Paper Reading | FastTrack: efficient and precise dynamic race detection

根据 AddressSanitizer, ThreadSanitizer, and MemorySanitizer: Dynamic Testing Tools for C++ (GTAC'2013)，TSan V2 使用的 fast happens-before 算法，类似于 FastTrack(PLDI'09) 中提出的算法。

本文是对 FastTrack: efficient and precise dynamic race detection (PLDI'09) 这篇论文的学习笔记。

Preliminaries

Data Race

在 FastTrack(PLDI'09) 论文中，全文都用的是 race condition，根据 Race Condition vs. Data Race. EMBEDDED IN ACADEMIA 中给出的关于 race condition 和 data race 的定义，该论文中应该实际指代的应该是 data race。本文全都使用 “data race” 。

首先看 data race 的定义：

即，如果两个线程访问同一个内存位置 (memory location)，至少有一个访问是写操作，并且两个线程访问内存位置的访问顺序是不确定，则说明存在 data race。

举一个非常简单的 data race 的例子：

#include <pthread.h>
#include <stdio.h>

int Global;

void *Thread1(void *x) {
  Global=1;
  return NULL;
}

void *Thread2(void *x) {
  Global=2;
  return NULL;
}

int main() {
  pthread_t t[2];
  pthread_create(&t[0], NULL, Thread1, NULL);
  pthread_create(&t[1], NULL, Thread2, NULL);
  pthread_join(t[0], NULL);
  pthread_join(t[1], NULL);
  printf("%d", Global);
}

执行上述代码，输出是不确定的：有时候是 1，有时候是 2。

Concepts

一个程序中有很多个线程，每一个线程用 $t \in Tid$ 表示，这些线程读写的变量用 $x \in Var$ 表示，锁用 $m \in Lock$ 表示。

线程 $t$ 能执行的操作包括：

happen-before 的定义（尝试用中文表述总觉得词不达意，摆烂直接用英文原文）：

A trace $\alpha$ captures an execution of a multithreaded program by listing the sequence of operations performed by the various threads.

The happens-before relation $<_\alpha$ for a trace $\alpha$ is the smallest transitively-closed relation over the operations in $\alpha$ such that the relation $a <_\alpha b$ holds whenever $a$ occurs before $b$ in $\alpha$ and one of the following holds:

如果 $a$ happens before $b$，那么 $b$ happens after $a$

如果两个线程访问同一个内存位置 (memory location)，至少有一个访问是写操作，并且这两个访问操作之间没有 happen-before 关系，那么说明这两个访存操作之间存在 data race。

Vector Clock and $DJIT^+$ Algorithm

Vector Clock

假设程序中有 n 个线程，每个线程都对应一个 n 个元素的 vector，称为 vector clock。

Vector clock 之间是存在偏序关系 $\sqsubseteq$ 的。

$\sqcup$ 表示两个 vector clock 之间的交汇 (join) 操作。

$\bot_C$ 表示最小的 vector clock 。

$inc_t$ 表示递增 vector clock 的表示线程 $t$ 的那个元素。

形式化表示如下：

举个例子帮忙理解 vector clock 。

假设程序中有 2 个线程 $t_1$ 和 $t_2$ ，假设 $t_1$ 的 vector clock $C_1$ 为 $<4, 0>$，$t_2$ 的 vector clock $C_2$ 为 $<5, 8>$ 。

$DJIT^+$ Algorithm

$DJIT^+$ Algorithm 就是基于 vector clock 来检测 data race 的：

我们用如下例子来理解 $DJIT^+$ 是如何检测 data race 的：

如上图所示，程序中有两个线程，线程 0 和线程 1。线程 0 对应的 vector clock 为 $\mathbb{C}_0$，线程 1 对应的 vector clock 为 $\mathbb{C}_1$，锁 $m$ 对应的 vector clock 为 $\mathbb{L}_m$，并且我们用 vector clock $\mathbb{W}_x$ 来记录前一次对变量 $x$ 的写操作。

  1. 初始状态时，$\mathbb{C}_0$ 为 <4, 0>，$\mathbb{C}_1$ 为 <0, 8>，$\mathbb{L}_m$ 为 <0, 0>（即 $\bot_C$），$\mathbb{W}_x$ 为 <0, 0>（即 $\bot_C$）

  2. 线程 0 写变量 $x$，vector clock $\mathbb{W}_x[0]$ 的值更新为 $\mathbb{C}_0[0]$ 的值，所以 $\mathbb{W}_x$ 的值由 <0, 0>更新为 <4, 0>，其余 vector clock 的值不变

  3. 线程 0 释放锁 $m$，vector clock $\mathbb{L}_m$ 的值更新为 $\mathbb{C}_0$ 的值 <4, 0>，然后 vector clock $\mathbb{C}_0$ 的值更新为 $inc_0(\mathbb{C}_0)$ 即 <5, 0>，其余 vector clock 的值不变

  4. 线程 1 获取锁 $m$，vector clock $\mathbb{C}_1$ 的值更新为 $\mathbb{C}_1 \sqcup \mathbb{L}_m$ 即 <0, 8> $\sqcup$ <4, 0> = <4, 8>，其余 vector clock 的值不变

  5. 线程 1 写变量 $x$，由于 $\mathbb{C}_1$ 为 <4, 8>，$\mathbb{W}_x$ 为 <4, 0>，所以 $\mathbb{W}_x\;\sqsubseteq\;\mathbb{C}_1$，也就是说 $\mathbb{wr(0, x)}\;\text{happen-before}\;\mathbb{wr(1, x)}$，所以线程 1 写变量 $x$ 与线程 0 写变量 $x$ 之间没有 data race。最后还要更新 $\mathbb{W}_x[1]$ 为 $\mathbb{C}_1[1]$ ，即 $\mathbb{W}_x$ 的值由 <4, 0> 变为 <4, 8>，其余 vector clock 的值不变

FastTrack Algorithm

上述基于 vector clock 的 $DJIT^+$ Algorithm 的缺点就是性能开销。如果程序中有 n 个线程，那么每一个 vector clock 都需要 $O(n)$ 的空间，并且对 vector clock 的操作 (copying, comparing, joining, etc) 都要花费 $O(n)$ 的时间。

key observation：作者通过收集大量的 Java 程序信息发现：在所有需要被 data race detector 监测的操作（$rd$, $wr$, $acq$, $rel$, $fork$, $join$, …）中，同步 (synchronization) 操作 (lock acquires and releases, forks, joins, waits, notifies, etc) 出现的次数只占很少的比例；而对数组和对象字段的读写则占了被监测操作的 96% 。

key insight：超过 99% 的读写操作，我们并不需要使用 vector clock 来表示其 happen-before 关系，只需使用一种更轻量级 happen-before 表示方式即可，只在必要时 fallback 为 vector clock 。

还是用上面这个例子来进行说明，这次我们不再使用 vector clock 来记录每个线程对变量 $x$ 的写操作，只记录上一次是哪个线程写了变量 $x$ ：

我们把 clock $c$ 和 thread $t$ 组成的对组 (pair) 叫作 $epoch$，记作 $c@t$。epoch 与 vector clock 存在如下关系：$c@t \preceq C\quad\textbf{iff}\quad c \leq C(t)$ 。

在上面这个例子中，对于 $\mathbb{W}_x$ 我们只需要使用 $epoch$ 记录上一次是哪个线程写了变量 $x$ ：

  1. 初始状态时，$\mathbb{C}_0$ 为 <4, 0>，$\mathbb{C}_1$ 为 <0, 8>，$\mathbb{L}_m$ 为 <0, 0>（即 $\bot_C$），$\mathbb{W}_x$ 为 $\bot_e$

  2. 线程 0 写变量 $x$，将 epoch $\mathbb{W}_x$ 的值更新为 $4@0$，表示线程 0 在 clock 为 4 时写了变量 $x$

  3. 线程 0 释放锁 $m$，vector clock $\mathbb{L}_m$ 的值更新为 $\mathbb{C}_0$ 的值 <4, 0>，然后 vector clock $\mathbb{C}_0$ 的值更新为 $inc_0(\mathbb{C}_0)$ 即 <5, 0>，其余 vector clock 的值不变

  4. 线程 1 获取锁 $m$，vector clock $\mathbb{C}_1$ 的值更新为 $\mathbb{C}_1 \sqcup \mathbb{L}_m$ 即 <0, 8> $\sqcup$ <4, 0> = <4, 8>，其余 vector clock 的值不变

  5. 线程 1 写变量 $x$，由于 $\mathbb{C}_1$ 为 <4, 8>，$\mathbb{W}_x$ 为 $4@0$，所以有 $\mathbb{W}_x=4@0 \preceq\;<4,8>\;=\mathbb{C}_1$，也就是说 $\mathbb{wr(0, x)}\;\text{happen-before}\;\mathbb{wr(1, x)}$，所以线程 1 写变量 $x$ 与线程 0 写变量 $x$ 之间没有 data race。最后还要更新 $\mathbb{W}_x$ 为 $8@1$，表示线程 1 在 clock 为 8 时写了变量 $x$，其余 vector clock 的值不变

在这个例子中，我们用 epoch 来代替 vector clock $\mathbb{W}_x$ 后，在判断 $wr(1, x)$ 是否与 $wr(0, x)$ 之间存在 data race 时，将 $O(n)$ 的 vector clock 之间的比较操作 $\sqsubseteq$ 替换优化为了 $O(1)$ 的 epoch 与 vector clock 之间的比较操作 $\preceq$ 。

下面我们系统地学习一下 FastTrack Algorithm 是如何检测 data race 的。

Type of Data Race

data race 可以根据观测到的读写操作的先后顺序可以分为以下三类：

Analysis Detail

FastTrack 是一个 online algorithm，对于被测程序，FastTrack 会维护一个程序状态 $\sigma$，每当程序执行一个操作 $a$ 时，FastTrack 会相应地更新状态：$\sigma \Rightarrow^a \sigma'$ 。

$\sigma=(C,L,R,W)$ 是一个四元组：

状态 $\sigma$ 的初始值为：

$\sigma_0 = (\lambda t. inc_t(\bot_V), \lambda m.\bot_V, \lambda x.\bot_e, \lambda x.\bot_e)$

$E(t)$ 表示线程 $t$ 的当前 epoch $c@t$，其中 $c=C_t(t)$ 即线程 $t$ 的当前 clock 。

$R$ 是一个函数，$R_x$ 是 $R(x)$ 的缩写，$R[x := V ]$ 表示将 $R(x)$ 修改为 $V$，其余部分不变。

下图详细给出了针对不同的操作，FastTrack 是如何更新程序状态 $\sigma$（在每种操作的右边同时给出了作者在 benchmarks 中观察到的不同操作的出现占比）：

Read Operations

Read Operations 又细分为 4 条规则：

Write Operations

Other Operations

Other operations包括 acquire, release, fork 和 join，FastTrack algorithm 对这些操作的处理与 $DJIT^+$ algorithm 类似：

Algorithm Pseudo Code

FastTrack Algorithm 的伪代码实现如下，就是对上一节 Analysis Detail 的实现，此处不再赘述：

Example

最后，我们再用一个例子来理解 FastTrack 是如何检测 data race 的：

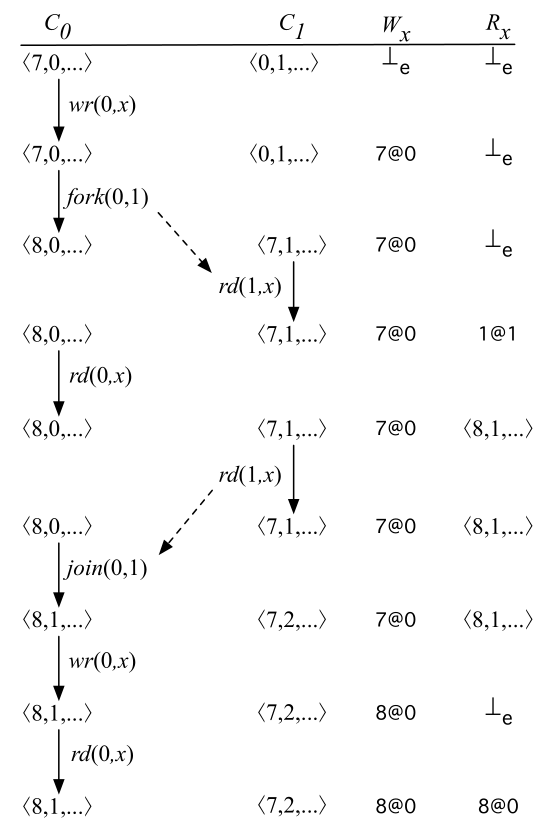
初始状态时，$W_x$ 和 $R_x$ 都是 $\bot_e$ ，表示变量 $x$ 还没有被写和读过。

  1. 线程 0 写变量 $x$，epoch $W_x$ 的值更新为线程 0 的当前 epoch $c@t$，即 $7@0$

  2. $fork(0, 1)$ 。先将 $C_1$ 的值更新为 $C_1 \sqcup C_0$ 即 <7,1>，再将 $C_0$ 的值更新为 $inc_0(C_0)$ 即 <8, 0>

  3. 线程 1 读变量 $x$，因为前一次对变量 $x$ 的写 happen-before 此时线程 1 对变量 $x$ 的读 ($W_x=7@0\preceq\;<7,1>\;=C_1$)，所有没有 write-read data race。 因为之前 $R_x$ 是 $\bot_e$，所以只需要用 epoch 来表示 $R_x$ 即可，将 $R_x$ 的值更新为线程 1 的当前 epoch $c@t$，即 $1@1$

  4. 线程 0 读变量 $x$，因为前一次对变量 $x$ 的写 happen-before 此时线程 0 对变量 $x$ 的读 ($W_x=7@0\preceq\;<8,0>\;=C_0$)，所有没有 write-read data race。但是前一次对变量 $x$ 的读与此时线程 0 对变量 $x$ 的读没有 happen-before 关系 ($R_x =1@1\npreceq\;<8,0>\;=C_0$) 。所以需要用 vector clock 替代 epoch 来表示 $R_x$ ，将 $R_x$ 的值更新为 <8, 1>

  5. 线程 1 读变量 $x$，因为前一次对变量 $x$ 的写 happen-before 此时线程 1 对变量 $x$ 的读 ($W_x=7@0\preceq\;<7,1>\;=C_1$)，所以没有 write-read data race。 因为 $R_x$ 已经是是 vector clock 表示了，所以只需要把 vector clock $R_x$ 中线程 1 的那部分更新为 $C_1(1)$ 即可。因为 $R_x(1)$ 是 1，$C_1(1)$ 也是 1，vector clock $R_x$ 更新前后都是 <8, 1>

  6. $join(0, 1)$，先将 $C_0$ 的值更新为 $C_0 \sqcup C_1$ 即 <8,1>，再将 $C_1$ 的值更新为 $inc_1(C_1)$ 即 <7, 2>

  7. 线程 0 写变量 $x$，此时 $R_x$ 已经是用 vector clock 表示的，并且前面所有对变量 $x$ 的读 happen-before 此时线程 0 对变量 $x$ 的写，没有 read-write data race ($R_x=\;<8,1>\;\sqsubseteq\;<8,1>\;=C_0$)，前一次对变量 $x$ 的写 happen-before 此时线程 $t$ 对变量 $x$ 的写，没有 write-write data race ($W_x =7@0\preceq\;<8,1>=C_0$)，我们把 $W_x$ 中更新为线程 0 的当前 epoch即 $8@0$ ，并且把 $R_x$ 更新为 $\bot_e$ 。

  8. 线程 0 读变量 $x$，因为前一次对变量 $x$ 的写 happen-before 此时线程 0 对变量 $x$ 的读 ($W_x=8@0\preceq\;<8,1>\;=C_0$)，所以没有 write-read data race。 因为之前 $R_x$ 是 $\bot_e$，所以只需要用 epoch 来表示 $R_x$ 即可，将 $R_x$ 的值更新为线程 0 的当前 epoch $c@t$，即 $8@0$

最终 FastTrack 发现程序中没有 data race 。

Conclusions

本文是对知名的 data race 检测算法 FastTrack 的学习笔记。

FastTrack 算法是对 $DJIT^+$ 算法的一个优化，本质上都是基于 vector clock 检测 data tace 的，FastTrack 通过（在某些情况下）使用 epoch 代替 vector clock 来获得更好的空间复杂度和时间复杂度。

最后说一下，由于手工验证 data race detector 检测出来的 data race 是不是误报是非常困难的，所以对于 data race 的检测，我们希望 data race detector 报告出来的 data race 都是真的，而不是误报。在实践中，我们通常会用动态分析来做 data race 的检测，保证没有误报，比如 TSan 就是 data race 的动态分析工具。

理解了 FastTrack 算法后，再去阅读 TSan 源码，理解 TSan 背后的算法就会变得容易些。下一篇文章就是 ThreadSanitizer 底层算法的基本原理。