Branch Probability Analysis in LLVM

本文分析 LLVM 中 Branch Probability Analysis 的实现。

0x0. Prologue

笔者最近学习了下 LLVM 中 Branch Probability Analysis 这个 pass，写一篇博客记录下。

本文基于 LLVM 18.1.6 这个版本，Branch Probability Analysis 这个 pass 的实现位于 llvm/lib/Analysis/BranchProbabilityInfo.cpp，从 commit history 来看该 pass 的变更不是很频繁。

在 LLVM IR 上，对于有多个后继的基本块，每一条到其后继基本块的边都关联一个概率，称之为分支概率 (branch probabilities) 。顾名思义，Branch Probability Analysis 的作用就是为这样的有多个后继的基本块计算分支概率。

可以通过 llvm/test/Analysis/BranchProbabilityInfo/basic.ll 这个测试用例，初步了解下 Branch Probability Analysis：

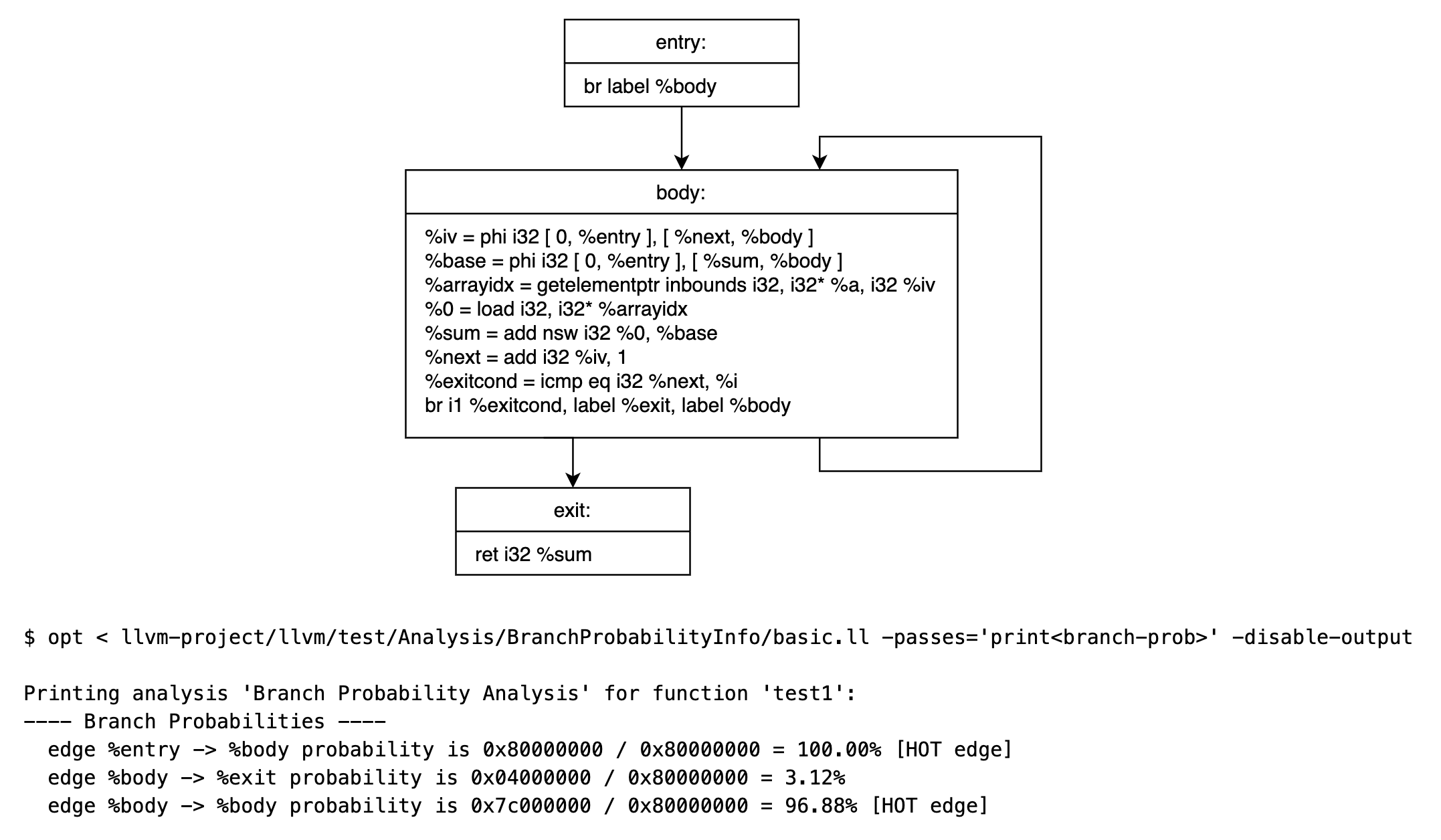
llvm/test/Analysis/BranchProbabilityInfo/basic.ll 中函数 test1() 的 Branch Probability Analysis 分析结果：

• %entry -> %body 的概率是 100%

• %body -> %exit 的概率是 3.12%

• %body -> %body 的概率是 96.88%

0x2. Algorithm & Implementation

prerequisite

Dominator 是程序分析中的基础概念，Branch Probability Analysis 算法中用到了 dominate 关系，所以先简要介绍下 dominate 关系。

这里直接用 wikipedia 上的例子来说明。下左图是一个示例 control-flow graph，下右图是其对应的 dominator tree。

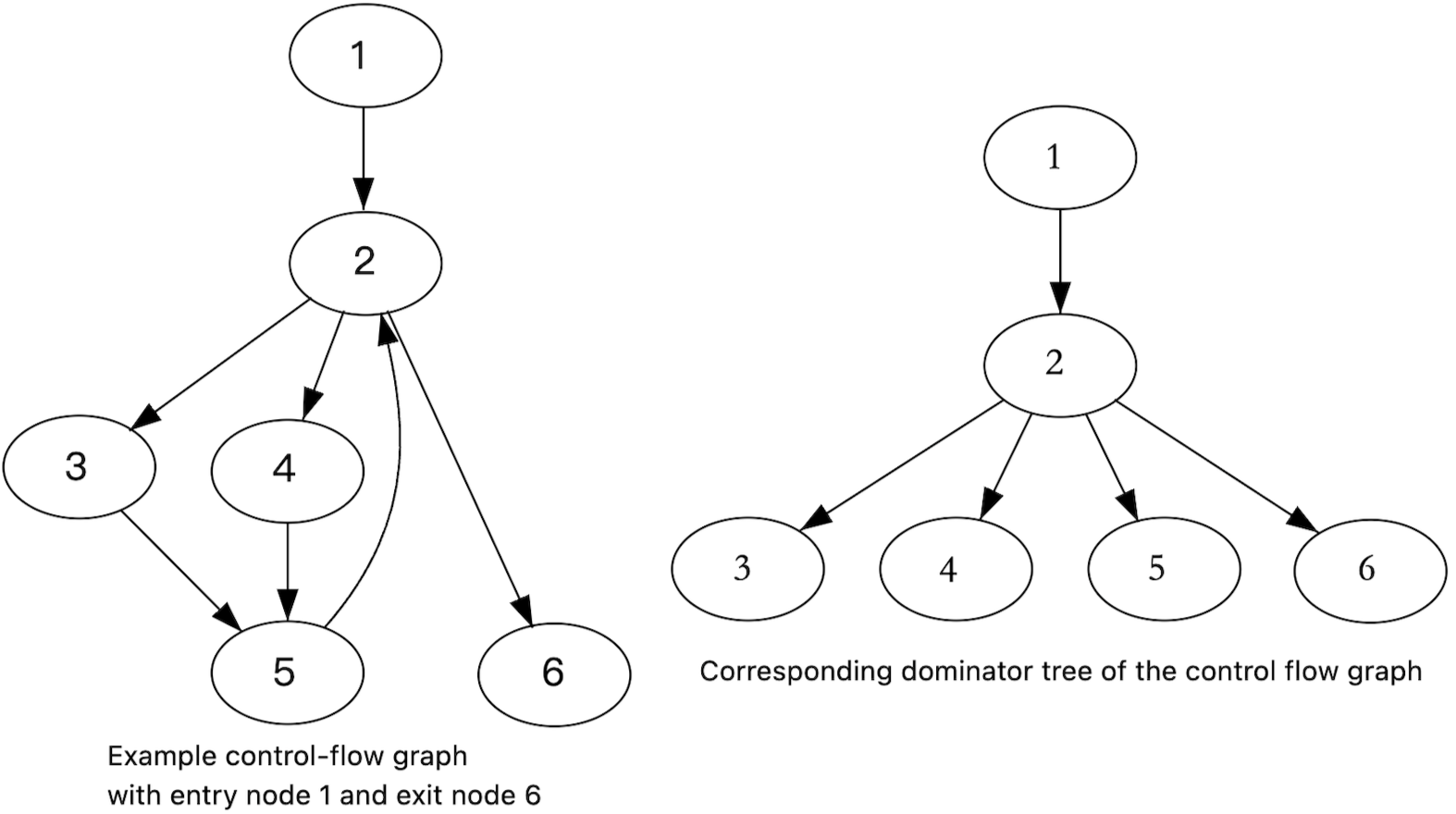
• 如果在 CFG 中每一条从入口节点到节点 $n$ 的路径都经过节点 $d$，则 $d$ dominates $n$，记作 $d$ dom $n$（每个节点 $n$ 都 dominates 自身）

• 如果 $d$ dom $n$ 且 $d \ne n$，则 $d$ strictly dominates $n$，记作 $d$ sdom $n$

• 如果 $d$ sdom $n$ 且不存在 $d’$ 使得 $d$ sdom $d’$ 且 $d’$ sdom $n$，则 $d$ immediately dominates $n$，记作 $d$ idom $n$。除了入口节点外，每个节点都有一个 immediate dominator

• dominator tree 的根结点就是 CFG 中的入口节点，dominator tree 中每个节点都 immediately dominates 其子节点，每个节点的父节点就是其 immediate dominator

• 如果在 CFG 中每一条从节点 $n$ 到出口节点的路径都经过节点 $z$，则 $z$ post-dominates $n$，记作 $z$ post-dom $n$（每个节点 $n$ 都 post-dominates 自身）。strictly post-dominates 和 immediately post-dominates 的定义不再赘述。

除了 dominator 外，Branch Probability Analysis 算法中还涉及到了循环的相关概念，https://llvm.org/docs/LoopTerminology.html 讲的非常清楚。

Intuition

在深入 Branch Probability Analysis 在 LLVM 中的实现之前，先考虑下这样一个问题：给定一段代码，有哪些信息可以帮助判断代码中分支被执行的概率？

1. 静态

   编译器提供了很多的 builtin functions，其中就有一些与分支预测相关的 builtin function，如：

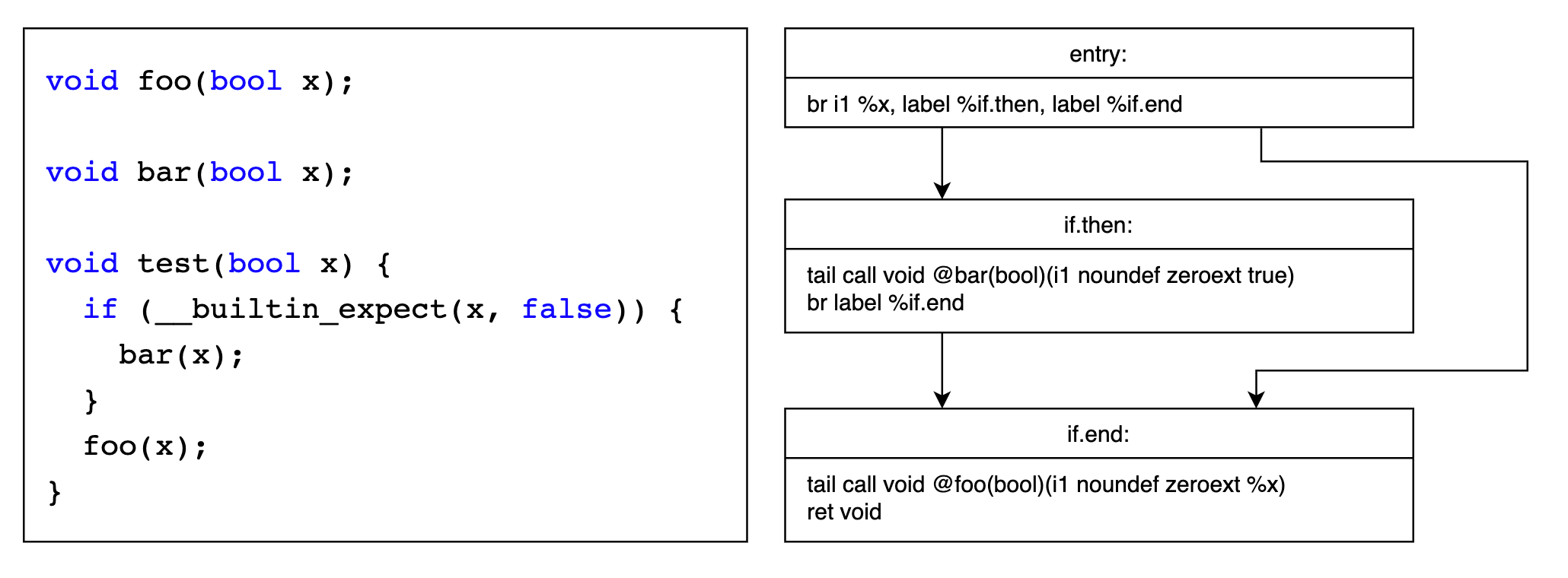
   • __builtin_expect(long exp, long c)，详见 GCC 和 Clang 的相关文档

     举个例子 https://godbolt.org/z/1asfGaGGM ，entry -> if.end 的概率应该为 ~100%

     

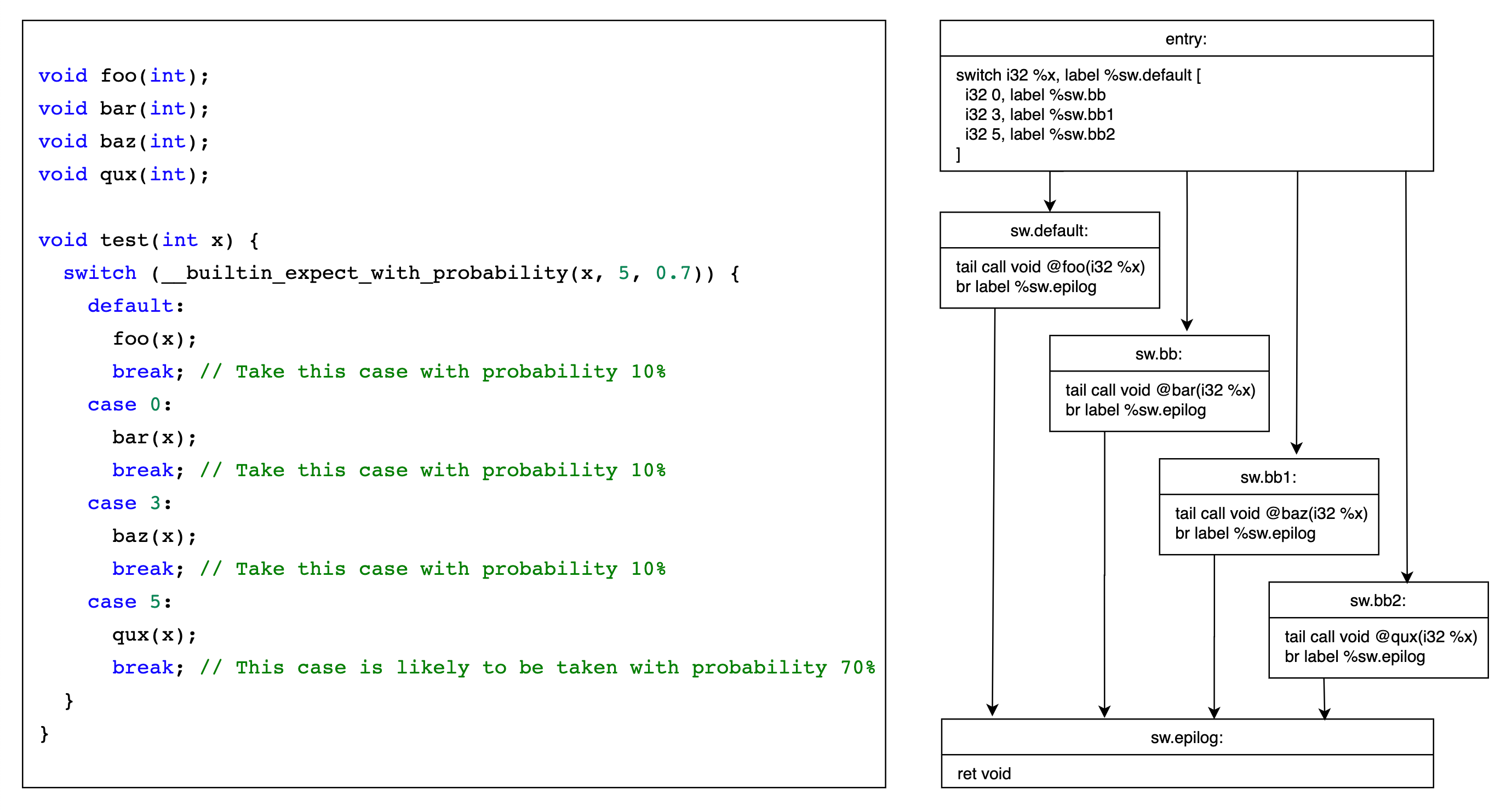
   • __builtin_expect_with_probability(long exp, long c, double probability)，详见 GCC 和 Clang 的相关文档

     举个例子 https://godbolt.org/z/96x5f43fs ，entry -> sw.bb2 的概率应该为 ~70%

     

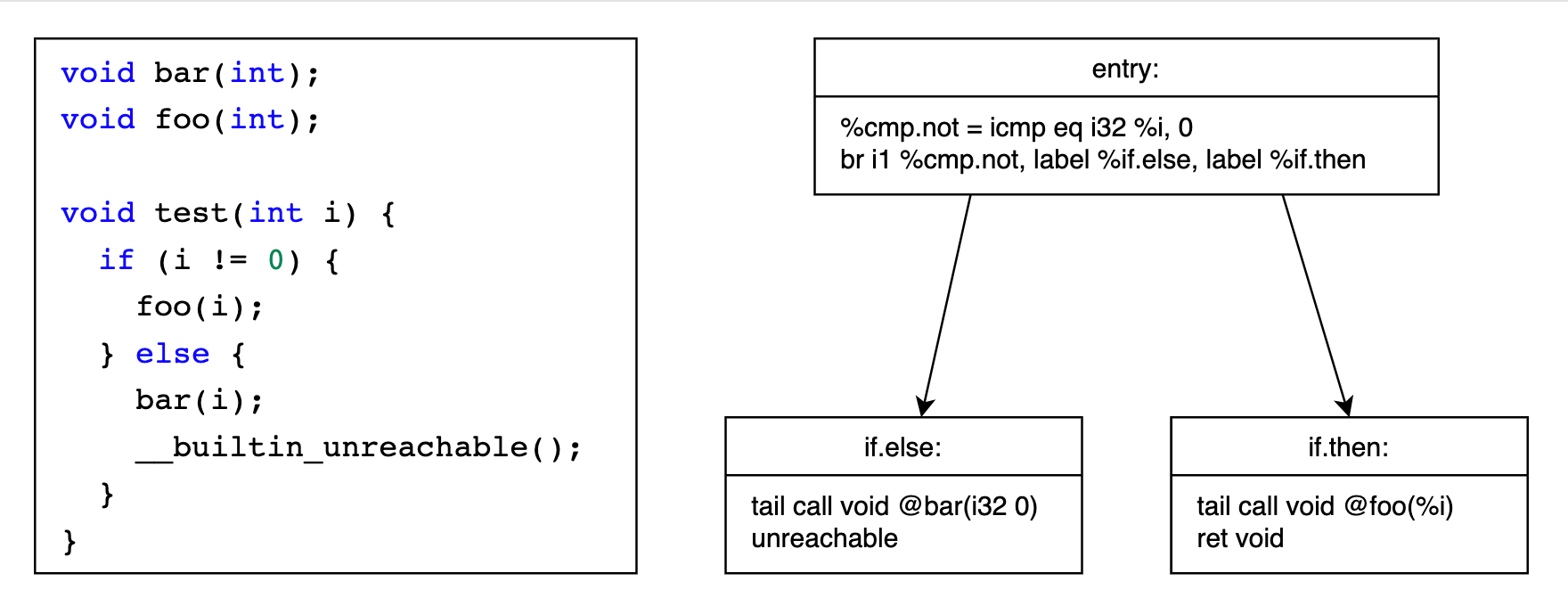
   • __builtin_unreachable()，详见 GCC 和 Clang 的相关文档

     举个例子 https://godbolt.org/z/bdd64xcvz ，entry -> if.else 的概率应该为 ~0%

     

2. 动态

   基于采样的反馈编译优化技术，如 AutoFDO，通过 perf 在程序运行时进行采样，然后指导编译器使用采样到的运行时信息进行优化。因此编译器可以根据采样到的运行时信息来判断代码中分支被执行的概率。 https://clang.llvm.org/docs/UsersManual.html#using-sampling-profilers

Algorithm

Branch Probability Analysis 的算法如下：

1. 为“初始”基本块设置权重，然后以这些“初始”基本块作为分析起点自底向上地设置函数内其他基本块的权重。

   “初始”基本块包括：

   • terminator instruction 是 unreachable instruction 的基本块。如果该基本块包含 call instruction 且 callee function 有 noreturn attribute，那么将该基本块的权重设置为 1，否则设置为 0。

   • 用于 exception handling 的基本块，如 landingpad instruction 所在的基本块。权重设置为 1。

   • 包含 call instruction 且 callee function 有 cold attribute 的基本块。权重设置为 0xffff。

   逆后序遍历函数中的基本块，为“初始”基本块设置权重。

   接下来我们会用到两个 WorkList：

   • BlockWorkList。对于 BlockWorkList 中保存的基本块，其后继基本块 successors 至少有一个被设置了权重。

   • LoopWorkList。对于 LoopWorkList 中保存的基本块，其所在循环的 exit blocks 至少有一个被设置了权重。

   对于被设置了权重的“初始”基本块 BB，我们构造一个集合 { BB, BB 的 immediately dominator, BB 的 immediately dominator 的 immediately dominator, … }，考虑集合中基本块 DomBB，如果 BB post-dominates DomBB，那么：

   • 如果 BB 不在 DomBB 所在的循环中（DomBB 属于某个循环并且 BB 不在该循环中），那么将 DomBB 加入到 LoopWorkList 中。

   • 如果 DomBB 与 BB 不在不同的循环中（DomBB 和 BB 不属于任何循环，或者 DomBB 和 BB 属于同一循环），那么设置 DomBB 的权重等于 BB 的权重。然后，对于 DomBB 的每一个前驱基本块 PredBB：如果 PredBB 属于某个循环且 DomBB 不在该循环中，那么将 PredBB 加入到 LoopWorkList 中；否则，将 PredBB 加入到 BlockWorkList 中。

   不断从 LoopWorkList 和 BlockWorkList 中 pop 基本块进行处理，直至 BlockWorkList 和 LoopWorkList 为空：

   • 给定两个基本块 SrcBB 和 DstBB，我们约定以 SrcBB 为起点以 DstBB 为终点的边 SrcBB -> DstBB （实际 CFG 上不一定存在 SrcBB -> DstBB 这样的边，我们构造这样的边只用于计算权重）的权重的计算方式如下：如果 DstBB 属于某个循环且 SrcBB 不在该循环中，那么 SrcBB -> DstBB 的权重就等于 DstBB 所在循环的权重；否则 SrcBB -> DstBB 的权重就等于 DstBB 这个基本块的权重。

   • 对于 LoopWorkList 中的基本块 BB，如果该基本块至其所在循环的所有 exit blocks 所构成的边都有权重，那么就将该循环的权重设置为这些边的权重的最大值，然后将该 BB 所在循环的 loop header 的前驱基本块都加入到 BlockWorkList 中。

   • 对于 BlockWorkList 中的基本块 BB，如果该基本块至其所有的后继基本块所构成的边都有权重，那么将该 BB 的权重设置为这些边的权重的最大值。然后，对于该 BB 的每一个前驱基本块 PredBB：如果 PredBB 属于某个循环且 BB 不在该循环中，那么将 PredBB 加入到 LoopWorkList 中；否则，将 PredBB 加入到 BlockWorkList 中。

   如果此时函数内还有基本块没有被设置权重，那么将这样的基本块的权重设置为 0xfffff。

2. 基于基本块的权重信息和启发式策略计算每个分支执行的概率。 后序遍历函数中的基本块，依次尝试以下启发式策略，一旦命中某个策略就不再尝试其他策略：

   1. 基于 branch weight metadata 计算当前基本块到其后继基本块的分支概率。前面提到 __builtin_expect, __builtin_expect_with_probability 和采样到的运行时信息都可以帮助判断代码中分支执行的概率，在 LLVM IR 上这些信息都是以 branch weight metadata 的形式记录在基本块的 terminator instruction 上的。因此，如果基本块的 terminator instruction 存在 branch weight metadata，那么就基于 branch weight metadata 计算该基本块到其后继基本块的分支概率。

   2. 基于基本块权重计算当前基本块到其后继基本块的分支概率。假设对于当前基本块 BB 存在三个后继基本块 Succ1, Succ2 和 Succ3，BB -> Succ1, BB -> Succ2 和 BB -> Succ3 这三条边的权重分别为 Weight1, Weight2 和 Weight3，那么 BB -> Succ1 分支的概率为 Weight1 / (Weight1 + Weight2 + Weight3)，BB -> Succ2 分支概率为 Weight2 / (Weight1 + Weight2 + Weight3)，BB -> Succ3 分支概率为 Weight3 / (Weight1 + Weight2 + Weight3)。

      如果在计算分支概率时，如果 BB -> Succ1 这条边有权重，但是 BB -> Succ2 和 BB -> Succ3 这两条边没有权重，那么会将 BB -> Succ2 和 BB -> Succ3 这两条边的权重视为默认值 0xfffff 参与计算分支概率。

      特别地，如果 BB 属于某个循环，Succ1 不在该循环中而 Succ2 和 Succ3 在该循环中，那么需要先将 BB -> Succ1 这条边的权重 Weight1 除以循环的 TripCount，然后再参与计算分支概率，这种情况下 BB -> Succ1 分支概率：(Weight1 / TripCount) / (Weight1 / TripCount + Weight2 + Weight3)，其中 TripCount 是一个编译时常量 31。

   3. 基于 pointer heuristics 计算当前基本块到其后继基本块的分支概率。如果当前基本块 BB 的 terminator instruction 是 conditional br instruction 即条件分支指令，且分支条件就是比较两个指针是否相等，相等时执行基本块 SuccEQ，不等时执行基本块 SuccNE，那么将 BB -> SuccEQ 的这一分支概率设置为 37.5%，将 BB -> SuccNE 这一分支概率设置为 62.5%。

   4. 基于 zero heuristics 计算当前基本块到其后继基本块的分支概率。如果当前基本块 BB 的 terminator instruction 是 conditional br instruction，

      • 如果分支条件是将 strcasecmp(), strcmp(), strncasecmp(), strncmp(), memcmp(), bcmp() 的返回值与整数常数作比较，相等时执行基本块 SuccEQ，不等时执行基本块 SuccNE，那么将 BB -> SuccEQ 的这一分支概率设置为 37.5%，将 BB -> SuccNE 这一分支概率设置为 62.5%。

      • 如果分支条件是判断是否等于常数 0，等于常数 0 时执行基本块 SuccEQ，不等于常数 0 时执行基本块 SuccNE，那么将 BB -> SuccEQ 的这一分支概率设置为 37.5%，将 BB -> SuccNE 这一分支概率设置为 62.5%。

      • 如果分支条件是判断小于常数 0 还是大于常数 0，小于常数 0 时执行基本块 SuccSLT，大于常数 0 时执行基本块 SuccSGT，那么将 BB -> SuccSLT 的分支概率设置为 37.5%，将 BB -> SuccSGT 分支概率设置为 62.5%。

   5. 基于 floating point heuristics 计算当前基本块到其后继基本块的分支概率。如果当前基本块 BB 的 terminator instruction 是 conditional br instruction，

      • 如果分支条件是判断两个浮点数是否相等，相等时执行基本块 SuccEQ，不等时执行基本块 SuccNE，那么将 BB -> SuccEQ 的这一分支概率设置为 37.5%，将 BB -> SuccNE 这一分支概率设置为 62.5%。

      • 如果分支条件是判断两个浮点数是否为 NaN，都不是 NaN 时执行基本块 SuccORD，至少有一个是 NaN 时执行基本块 SuccUNO，那么将 BB -> SuccORD 这一分支概率设置为 (1024 * 1024 - 1) / (1024 * 1024)，将 BB -> SuccUNO 这一分支分支概率为 1 / (1024 * 1024)。

0x3. Case study

Case 1: estimated block weight heuristics

https://godbolt.org/z/Ezn17o44z

通过本例来理解基于基本块权重计算当前基本块到其后继基本块的分支概率。

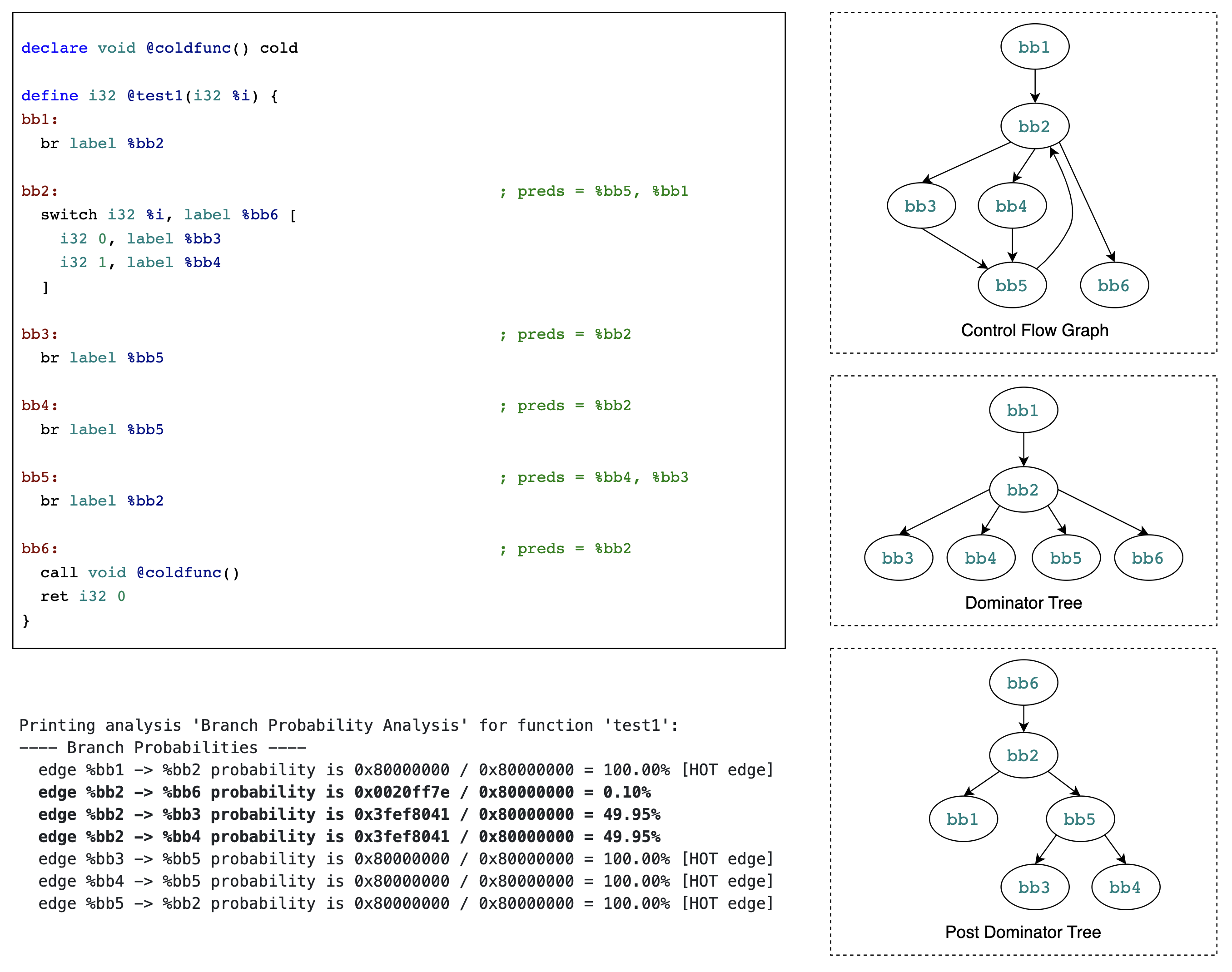
1. 逆后序遍历函数中的基本块，为“初始”基本块设置权重。本例子中只有一个“初始”基本块 BB6，因为 BB6 包含 call instruction 并且其 callee function 有 cold attribute，所以将 BB6 的权重设置为 0xffff。

   考虑 { BB6, BB6 的 immediately dominator, BB6 的 immediately dominator 的 immediately dominator, … } 这一集合中的基本块：

   1. BB6。显然 BB6 post-dominates BB6 自己。BB6 和 BB6 肯定不在不同的循环中（废话，他们是同一个基本块），所以设置 BB6 的权重等于 BB6 的权重。然后考虑 BB6 的前驱基本块，因为 BB6 只有一个前驱基本块 BB2，且 BB2 属于循环 {BB2, BB3, BB4, BB5}，而 BB6 不在该循环中，所以将 BB2 加入到 LoopWorkList 中。

   2. BB6 的 immediately dominator 是 BB2。根据 post dominator tree，BB6 post-dominates BB2。因为 BB6 不在 BB2 所属的循环中，所以将 BB2 放入 LoopWorkList 中。

   3. BB2 的 immediately dominator 是 BB1。根据 post dominator tree，BB6 post-dominates BB1。因为 BB1 和 BB6 不在不同的循环中，所以设置 BB1 的权重等于 BB6 的权重即 0xffff。因为 BB1 没有任何前驱基本块，所以不用考虑将 BB1 的前驱基本块加入到 LoopWorkList 或 BlockWorkList 中。

   接下来不断从 LoopWorkList 和 BlockWorkList 中 pop 基本块进行处理，直至 BlockWorkList 和 LoopWorkList 为空：

   1. 初始时 BlockWorkList 为空，所以无需遍历 BlockWorkList。

   2. LoopWorkList 有两个元素，都是 BB2。 从 LoopWorkList 中 pop 出第一个 BB2 进行处理，为 BB2 所在的循环设置权重。因为 BB2 所在的循环只有一个 exit block 即 BB6，所以如果 BB2 -> BB6 这条边有权重，那么 BB2 所在循环的权重就是 BB2 -> BB6 这条边的权重。回顾下，边的权重计算方式，因为 BB6 不属于任何循环，所以 BB2 -> BB6 这条边的权重就是 BB6 的权重即 0xffff，所以 BB2 所在循环的权重就是 0xffff。然后，将 BB2 所在循环的 loop header 的前驱基本块加入 BlockWorkList，即将 BB1 和 BB5 加入 BlockWorkList。 从 LoopWorkList 中 pop 出第二个 BB2 进行处理，因为已经为 BB2 所在的循环设置过权重，所以不再重复处理。

   3. 此时 BlockWorkList 中的元素是 BB1 和 BB5。 从 BlockWorkList 中 pop 出 BB1 进行处理。因为 BB1 的权重已经在之前被设置过了，所以跳过 BB1。 从 BlockWorkList 中 pop 出 BB5 进行处理。因为 BB5 只有一个后继基本块 BB2，所以 BB5 的权重就是 BB5 -> BB2 这条边的权重。虽然 BB2 位于循环中，但是 BB5 与 BB2 属于同一个循环，所以 BB5 -> BB2 这条边的权重就是 BB2 的权重，又因为 BB2 没有被设置权重，所以也就无法计算 BB5 -> BB2 这条边的权重，因此就无法设置 BB5 的权重。

   4. 至此，LoopWorkList 和 BlockWorkList 都为空。基本块只有 BB1 和 BB6 被设置了权重，都是 0xffff。循环 {BB2, BB3, BB4, BB5} 也被设置了权重，为 0xffff。

2. 后序遍历函数中的基本块，计算分支概率。因为各基本块的 terminator instruction 都没有存在 branch weight metadata，所以尝试基于基本块权重计算分支概率。

   因为 BB6 没有后继基本块，所以无需计算分支概率。因为 BB5、BB3、BB4、BB1 都只有一个后继基本块，所以也无需计算分支概率。 BB2 有三个后继基本块 BB6、BB3 和 BB4。BB2 -> BB6 的权重：BB2 -> BB6 的权重是 0xffff，但是因为 BB2 属于循环，而 BB6 不在该循环中，所以需要除以循环的 TripCount 31，变为 2114。BB2 -> BB3 的权重为默认值 0xfffff 即 1048575。BB2 -> BB4 的权重也是默认值 0xfffff 即 1048575。

   BB2 -> BB6 的概率为 2114 / (2114 + 1048575 + 1048575) = 0.10%

   BB2 -> BB3 的概率 1048575 / (2114 + 1048575 + 1048575) = 49.95%

   BB2 -> BB4 的概率 1048575 / (2114 + 1048575 + 1048575) = 49.95%

Case 2: branch weight metadata

https://godbolt.org/z/sEYqKMcbW

通过本例来理解基于 branch weight metadata 计算当前基本块到其后继基本块的分支概率。

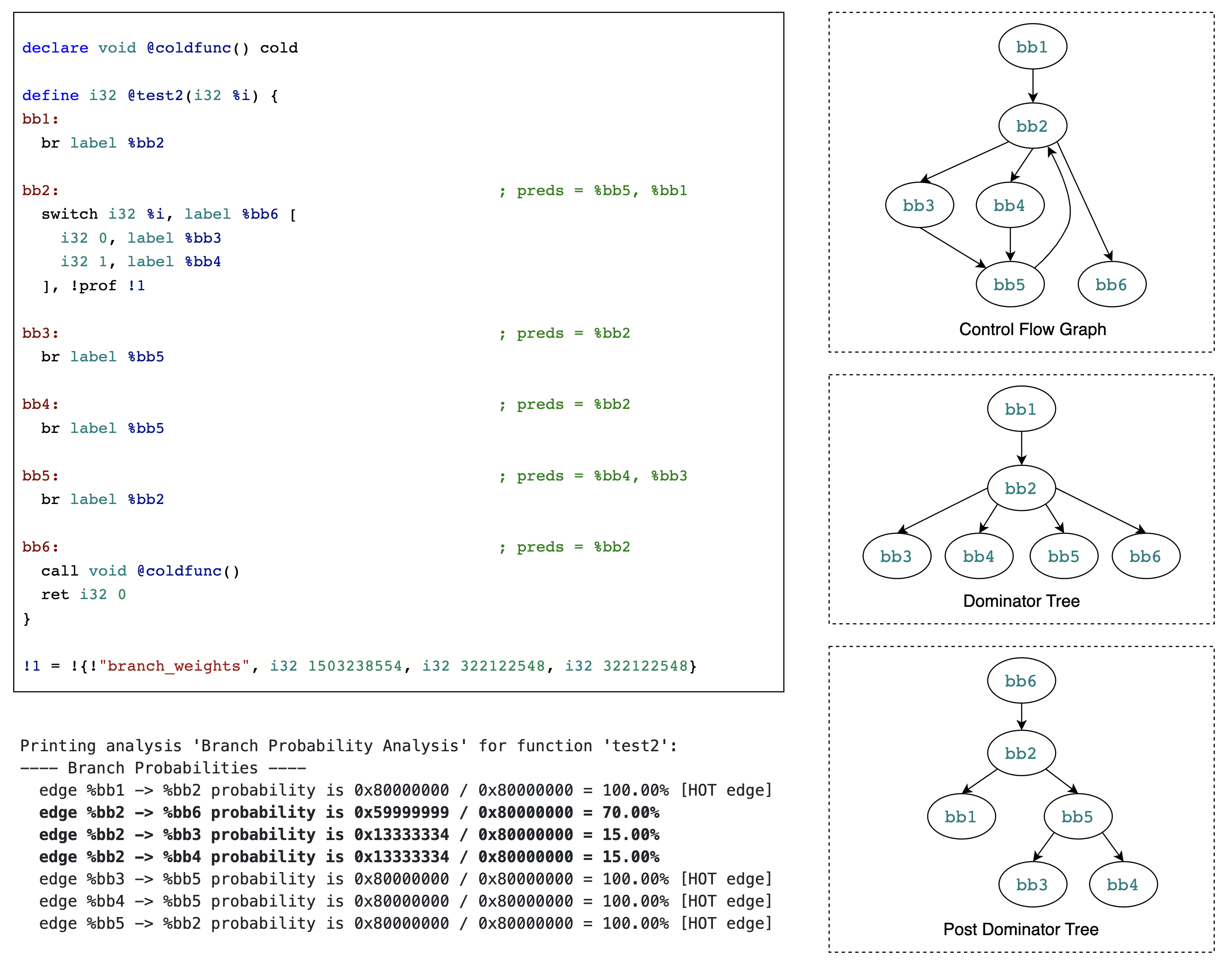
case 2 以“初始”基本块作为分析起点自底向上地设置函数内其他基本块的权重这一过程与 case 1 完全一样，省略。

与 case 1 不同的是，case 2 的 基本块 BB2 的 terminator instruction 存在 branch weight metadata，所以基本块 BB2 到其后继基本块的分支概率是基于 branch weight metadata 来计算的。

BB2 -> BB6 的概率：1503238554 / (322122548 + 322122548 + 1503238554) = 75%

BB2 -> BB3 的概率：1503238554 / (322122548 + 322122548 + 1503238554) = 15%

BB2 -> BB4 的概率：1503238554 / (322122548 + 322122548 + 1503238554) = 15%

Case 3: pointer heuristics

https://godbolt.org/z/szrx5nKvj

通过本例来理解基于 pointer heuristics 计算当前基本块到其后继基本块的分支概率

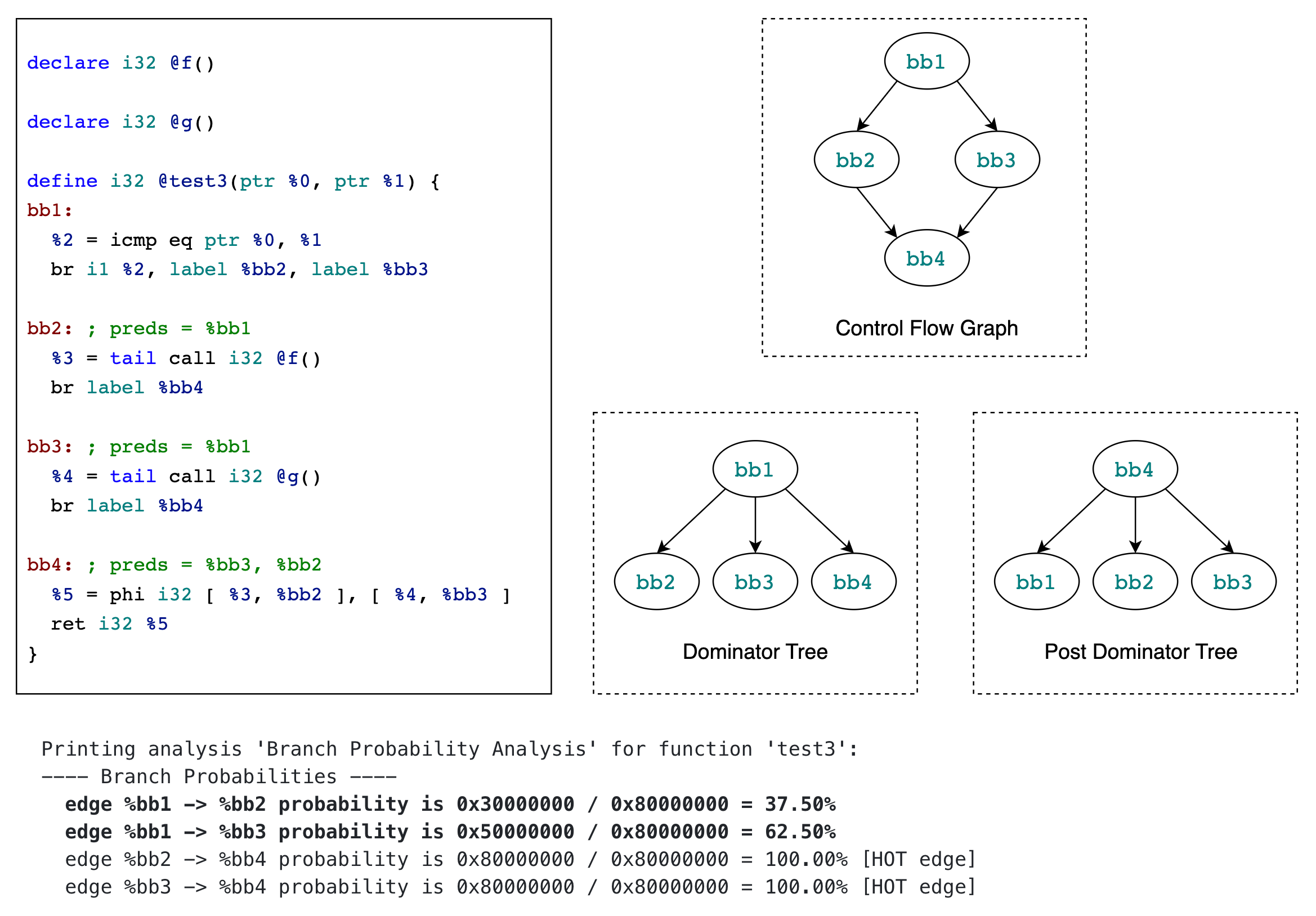
本例中没有“初始”基本块，所以也就没有以“初始”基本块作为分析起点自底向上地设置函数内其他基本块的权重这一过程。

注意到基本块 BB1 的 terminator instruction 是 conditional br instruction，且分支条件就是比较两个指针是否相等，相等时执行基本块 BB2，不等时执行基本块 BB3，所以根据 pointer heuristics，BB1 -> BB2 的概率为 37.5%，BB1 -> BB3 的概率为 62.5%。

Case 4: zero heuristics

https://godbolt.org/z/szY55EnMx

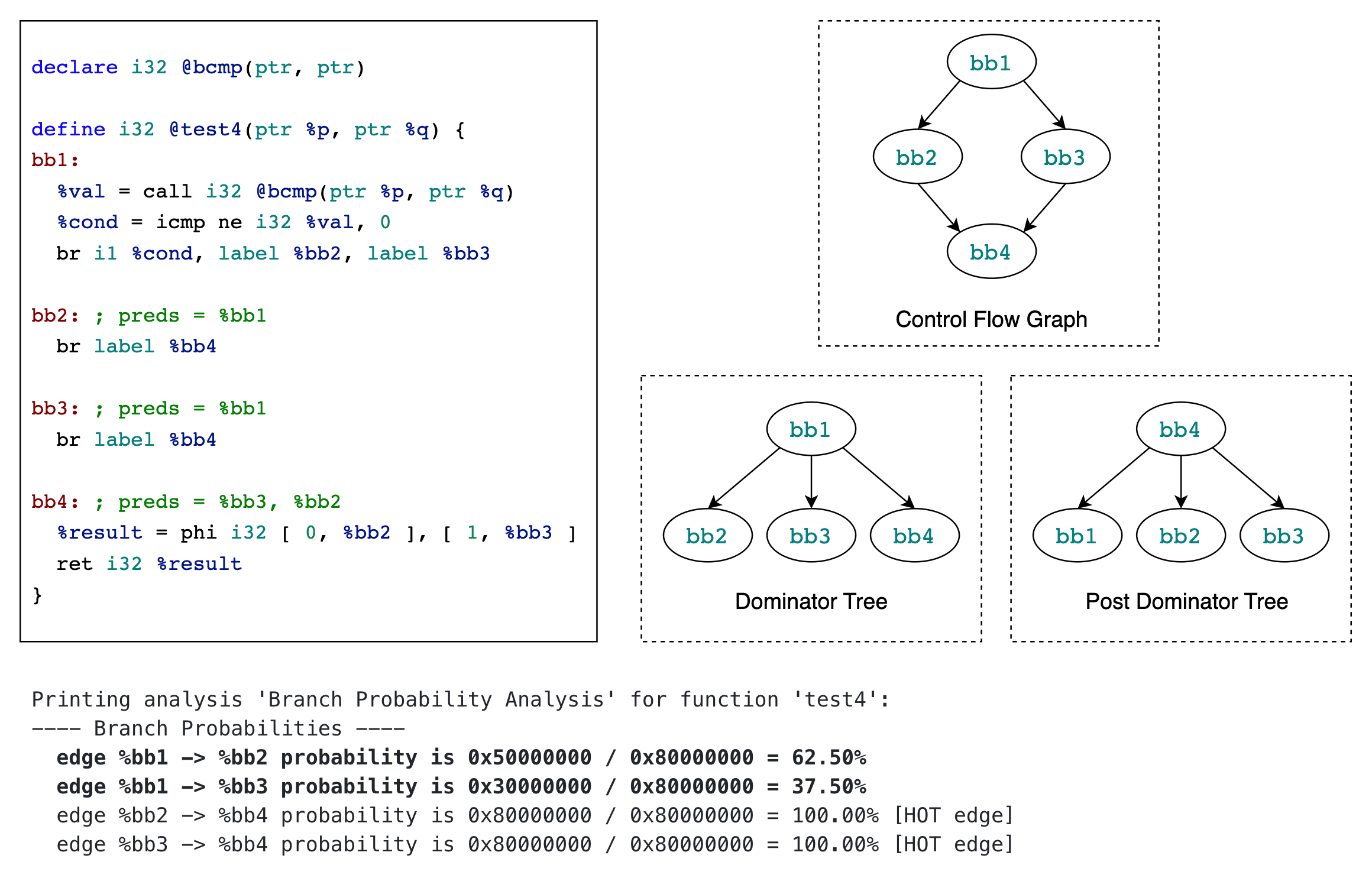
本例中没有“初始”基本块，所以也就没有以“初始”基本块作为分析起点自底向上地设置函数内其他基本块的权重这一过程。

注意到基本块 BB1 的 terminator instruction 是 conditional br instruction，且分支条件是将 bcmp() 的返回值与常数 0 作比较，不相等时执行基本块 BB2，相等时执行基本块 BB3，所以根据 zero heuristics，BB1 -> BB2 的概率为 62.5%，BB1 -> BB3 的概率为 37.5% 。

Case 5: floating point heuristics

https://godbolt.org/z/Ybn7PPEad

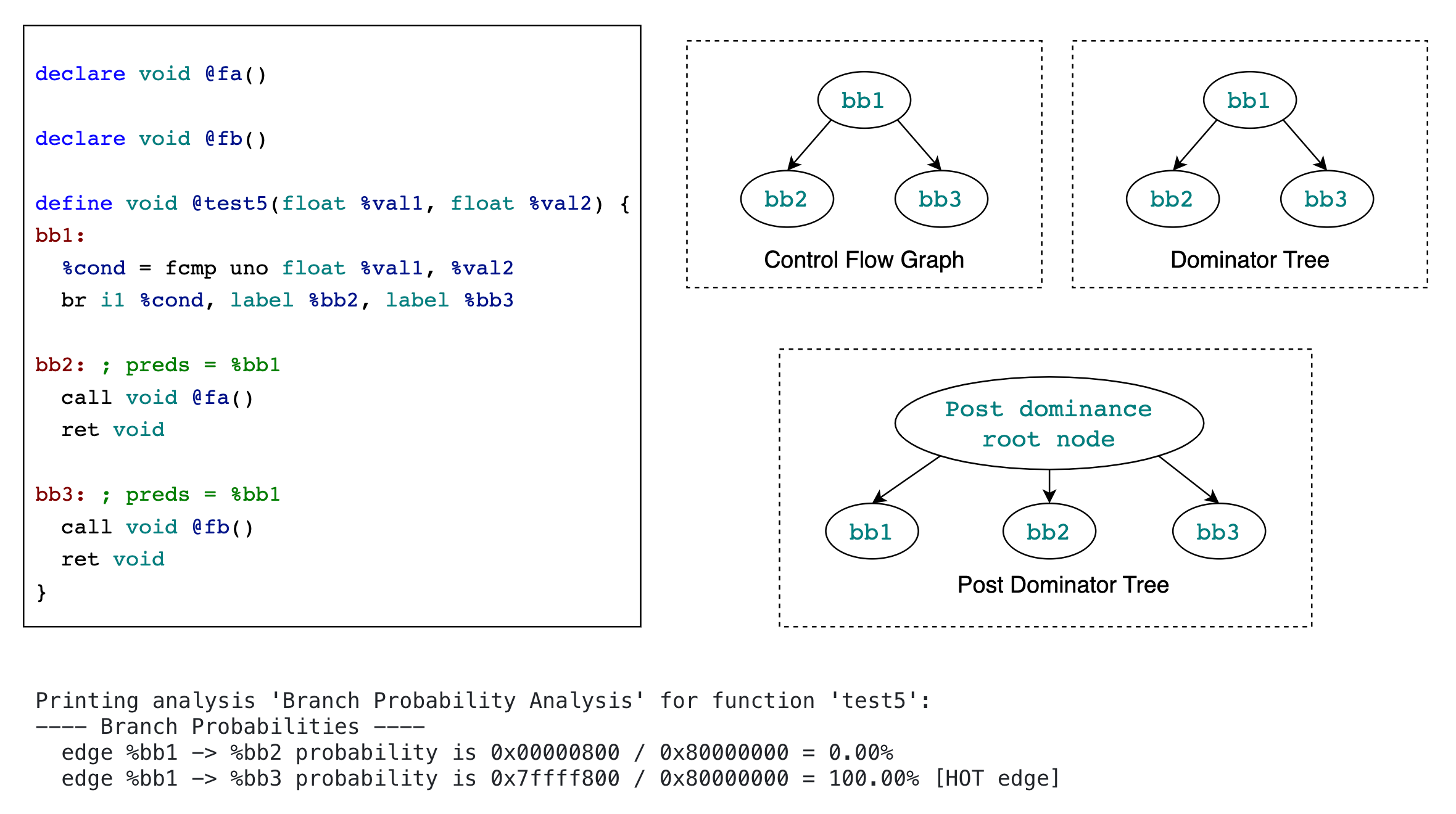
注：本例中 BB1, BB2 和 BB3 之间没有 post-dominates 关系。

本例中没有“初始”基本块，所以也就没有以“初始”基本块作为分析起点自底向上地设置函数内其他基本块的权重这一过程。

基本块 BB1 的 terminator instruction 是 conditional br instruction，分支条件是判断是否至少有一个浮点数为 NaN，如果是执行基本块 BB2，否则执行基本块 BB3，所以根据 zero heuristics，BB1 -> BB2 的概率为 1 / (1024 * 1024) = 0%，BB1 -> BB3 的概率为 (1024 * 1024 - 1) / (1024 * 1024) = 100% 。

0x4. getResult

在前面几节，我们介绍了 Branch Probability Analysis 的算法，知道了 CFG 上各分支概率是如何计算得到的。在本节，我们介绍 LLVM 中其他 pass 如何使用 Branch Probability Analysis 的分析结果。

对 Branch Probability Analysis 这个 pass 分析结果的使用分为两类：一类就是基于 Branch Probability Analysis 的分析结果来做编译优化；另一类则是在对 LLVM IR 进行变换后，必要时需要更新 Branch Probability Analysis 的分析结果。

1. 使用 BranchProbabilityAnalysis

   • BFI, llvm/lib/Analysis/InlineCost.cpp

     直接使用 Branch Probability Analysis 的分析结果的地方不多，大多都是直接使用 Block Frequency Analysis 的分析结果，而 Block Frequency Analysis 则依赖 Branch Probability Analysis 的分析结果（未来如果有时间，写一篇文章深入分析下 Block Frequency Analysis 的实现）。

     例如 bool InlineCostCallAnalyzer::isColdCallSite() 的实现：在没有运行时 profile 信息时，是通过 BlockFrequencyInfo(Block Frequency Analysis) 来判断给定的一个函数调用 callsite 是否为 cold callsite 的。

     bool InlineCostCallAnalyzer::isColdCallSite(CallBase &Call,
                                                 BlockFrequencyInfo *CallerBFI) {
       // If global profile summary is available, then callsite's coldness is
       // determined based on that.
       if (PSI && PSI->hasProfileSummary())
         return PSI->isColdCallSite(Call, CallerBFI);
     
       // Otherwise we need BFI to be available.
       if (!CallerBFI)
         return false;
     
       // Determine if the callsite is cold relative to caller's entry. We could
       // potentially cache the computation of scaled entry frequency, but the added
       // complexity is not worth it unless this scaling shows up high in the
       // profiles.
       const BranchProbability ColdProb(ColdCallSiteRelFreq, 100);
       auto CallSiteBB = Call.getParent();
       auto CallSiteFreq = CallerBFI->getBlockFreq(CallSiteBB);
       auto CallerEntryFreq =
           CallerBFI->getBlockFreq(&(Call.getCaller()->getEntryBlock()));
       return CallSiteFreq < CallerEntryFreq * ColdProb;
     }
     

   • BPI, llvm/lib/Transforms/Instrumentation/CFGMST.h, buildEdges()

     这里给出一处直接使用 Branch Probability Analysis 的分析结果的地方：给定一个 CFG 构建最小生成树 Minimum Spanning Tree 时使用了该信息。

     LLVM 中为 CFG 构建最小生成树的两个地方：

     • llvm/lib/Transforms/Instrumentation/GCOVProfiling.cpp

     • llvm/lib/Transforms/Instrumentation/PGOInstrumentation.cpp

2. 更新 BranchProbabilityAnalysis

   例如 InstCombine 这一优化 pass 可能会修改 branch condition，所以需要更新 Branch Probability Analysis 的分析结果，详见 https://github.com/llvm/llvm-project/pull/86470 。

0x5. MachineBranchProbabilityInfo

在 LLVM IR BasicBlock 这一层有 BranchProbabilityInfo，在 MachineBasicBlock 层有 MachineBranchProbabilityInfo ，其实现位于 llvm/lib/CodeGen/MachineBranchProbabilityInfo.cpp。 MachineBranchProbabilityInfo 是一个 ImmutablePass，只有 getEdgeProbability() 的接口，没有 setEdgeProbability() 的接口。

那么 MachineBranchProbabilityInfo 是在什么时候设置的呢？答案：是从 LLVM IR 转换为 SelectionDAG IR 创建 MachineBasicBlock 时基于 BranchProbabilityInfo 设置的，并且保存在 MachineBasicBlock 的成员变量 std::vector<BranchProbability> Probs 中，该成员变量记录了当前 MachineBasicBlock 至其后继的分支概率信息。了解更多信息，可以学习 https://reviews.llvm.org/D13745 。

MachineBlockPlacement pass 会基于 MachineBranchProbabilityInfo 做 Basic Block Code Layout optimization。

0x6. References

• https://llvm.org/docs/BranchWeightMetadata.html

• https://llvm.org/docs/BlockFrequencyTerminology.html

0x7. Epilogue

2024 第二季度只写了这一篇博客。

胡适之啊胡适之！你怎么能如此堕落！先前订下的学习计划你都忘了吗？子日：“吾日三省吾身。”不能再这样下去了！

眨眼间就要工作满三年了，这三年在工作生活上，我收获了很多，也失去了很多，准备写一篇博客好好回顾下这三年。对了！好久没有录播客了，说不定会录一期播客聊一聊！