SLP Vectorizer: Part 1 - Implementation in LLVM
本文分析 LLVM 的 SLP Vectorizer 实现。
Introduction
笔者之前写过一篇《Exploiting Superword Level Parallelism with Multimedia Instruction Sets》论文阅读笔记,文章最后留了一个坑:学习 LLVM 的 SLP Vectorizer 实现,现在来填坑。
LLVM SLP Vectorizer 于 LLVM 3.3 引入,于 LLVM 3.4 默认开启。本文对 LLVM SLP Vectorizer 的源码分析基于 LLVM release/4.x 版本。
P.S. 笔者在阅读 LLVM SLP Vectorizer 代码时,最开始时选择的是 release/16.x 版本的 SLP Vectorizer 代码,阅读了一段时候后发现 release/16.x 版本的 SLP Vectorizer 代码太复杂了。所以为了方便理解 LLVM SLP Vectorizer 的原理和实现,选取了 LLVM 的一个早期版本 release/4.x,在掌握了 LLVM release/4.x 版本的 SLP Vectorizer 实现后,再去看 LLVM 最新版本的 SLP Vectorizer 实现会变得容易很多。
Overview of the bottom-up SLP algorithm
GCC 与 LLVM 中 SLP Vectorizer 的实现都基于 bottom-up SLP algorithm (I. Rosen, D. Nuzman, and A. Zaks, “Loop-aware SLP in GCC,” in GCC Developers Summit, 2007.),GCC 添加 SLP Vectorizer 支持的 patch 见 Ira Rosen - [patch] Loop-aware SLP。
Bottom-up SLP algorithm 的流程如下图所示:
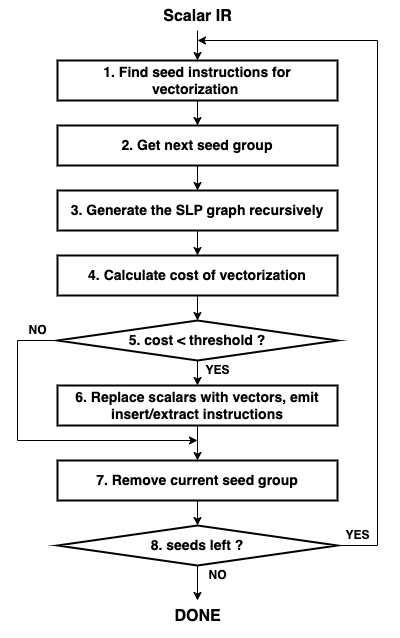
扫描编译器的中间表示,识别特定类型的指令集合。这些指令集合被称为种子,指的是很有可能转换为向量化指令的相同类型的指令集合。例如:访问相邻内存位置且没有依赖的 store 指令。
从种子指令集合 work-list 中选出一组种子作为 SLP 图的根节点。SLP 图的每个节点都是一组可向量化的标量指令。
从根节点出发,沿着 use-def 链不断添加节点至 SLP 图中,直至访问到一组不能向量化的指令。
在 SLP 图构建完成后,需要估算向量化后的代码是否有性能优势。基于编译器的 target-specific cost model,估算向量化后的代码在运行时的指令开销,与原本的标量指令在运行时的指令开销对比, SLP cost = 向量化后的代码在运行时的指令开销 - 原本的标量指令在运行时的指令开销,SLP cost 越小说明向量化的性能收益越大。
将上一步计算出的 SLP cost 与阈值(通常为 0)进行比较,以确定是否向量化。
如果进行向量化,编译器会修改中间表示,用等效的向量指令替换原本的标量指令,并生成向量和标量指令之间数据流所需的 insert 或 extract 指令。
从种子指令集合 work-list 中删除当前这组种子,并对种子集合 work-list 中剩余的种子重复该向量化过程。
举例说明 Bottom-up SLP algorithm 的流程。
考虑如下代码:
int a[4], b[4], c[4], d[4], e[4];
void foo() {
a[0] = (b[0] + c[0]) * (d[0] - e[0]);
a[1] = (b[1] + c[1]) * (d[1] - e[1]);
a[2] = (b[2] + c[2]) * (d[2] - e[2]);
a[3] = (b[3] + c[3]) * (d[3] - e[3]);
}
本例中,种子指令集合就是访问相邻内存位置且没有依赖的 store 指令:{a[0]=..., a[1]=..., a[2]=..., a[3]=...}。构建出的 SLP 图如下所示:
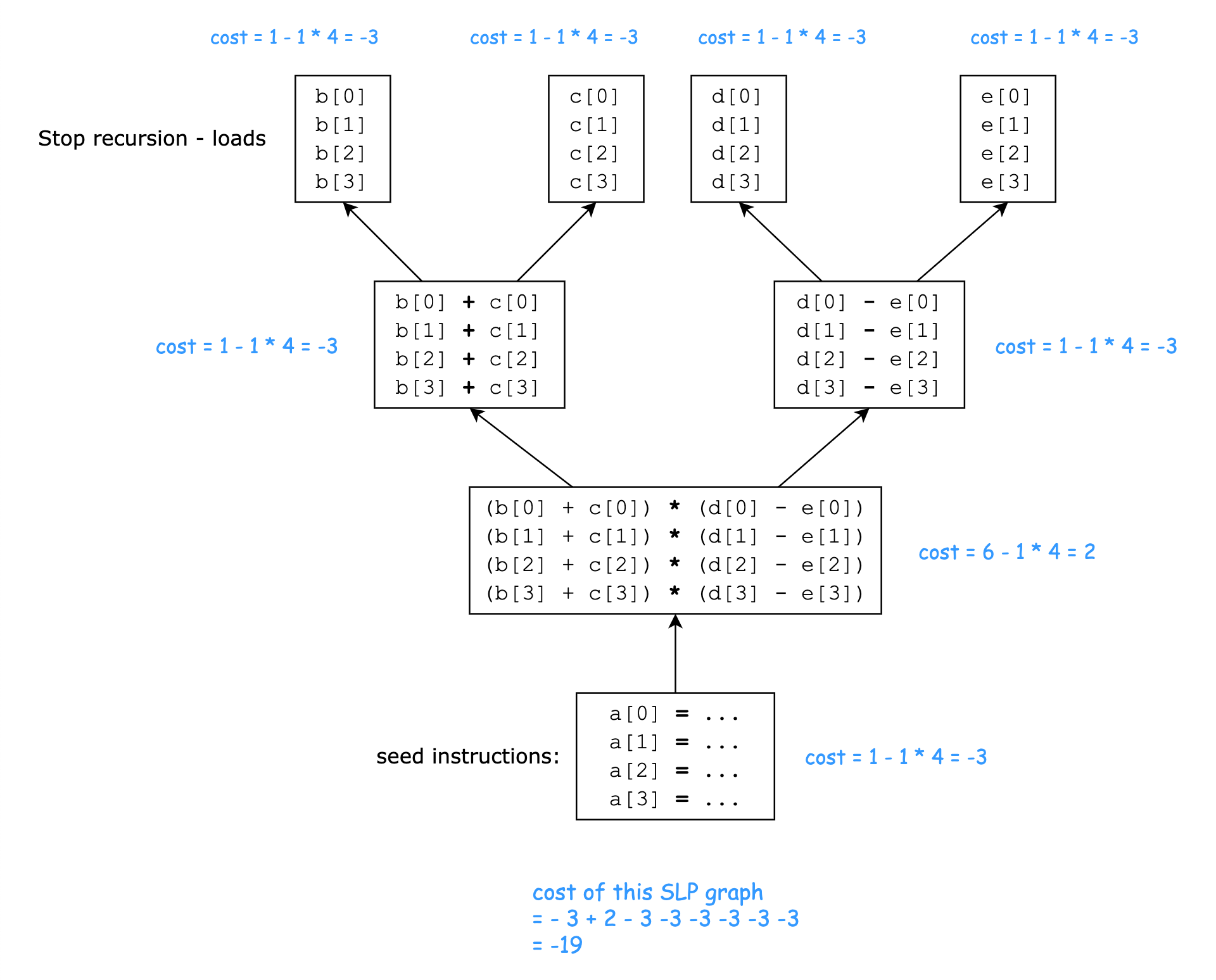
假设:
对于 load/store 指令,无论是标量指令还是向量指令,一条 load/store 指令 的 cost 都是 1
对于 add/sub 指令,无论是标量指令还是向量指令,一条 add/sub 指令 的 cost 都是 1
对于 mul 指令,一条标量 mul 指令的 cost 为 1,一条向量 mul 指令的 cost 为 6
据此假设,向量化后的代码在运行时的指令开销 - 原本的标量指令在运行时的指令开销 = -19,即向量化是存在性能收益的,因此会进行向量化。
可以通过 https://godbolt.org/z/x6MTqfb73 看到未经向量化生成的汇编代码和经 SLP 向量化后生成的汇编代码。
未经向量化的汇编 (Intel asm syntax) 如下:
foo(): # @foo() mov eax, dword ptr [rip + b] add eax, dword ptr [rip + c] mov ecx, dword ptr [rip + d] sub ecx, dword ptr [rip + e] imul eax, ecx mov dword ptr [rip + a], eax mov eax, dword ptr [rip + b+4] add eax, dword ptr [rip + c+4] mov ecx, dword ptr [rip + d+4] sub ecx, dword ptr [rip + e+4] imul eax, ecx mov dword ptr [rip + a+4], eax mov eax, dword ptr [rip + b+8] add eax, dword ptr [rip + c+8] mov ecx, dword ptr [rip + d+8] sub ecx, dword ptr [rip + e+8] imul eax, ecx mov dword ptr [rip + a+8], eax mov eax, dword ptr [rip + b+12] add eax, dword ptr [rip + c+12] mov ecx, dword ptr [rip + d+12] sub ecx, dword ptr [rip + e+12] imul eax, ecx mov dword ptr [rip + a+12], eax retSLP 向量化后的汇编代码如下:
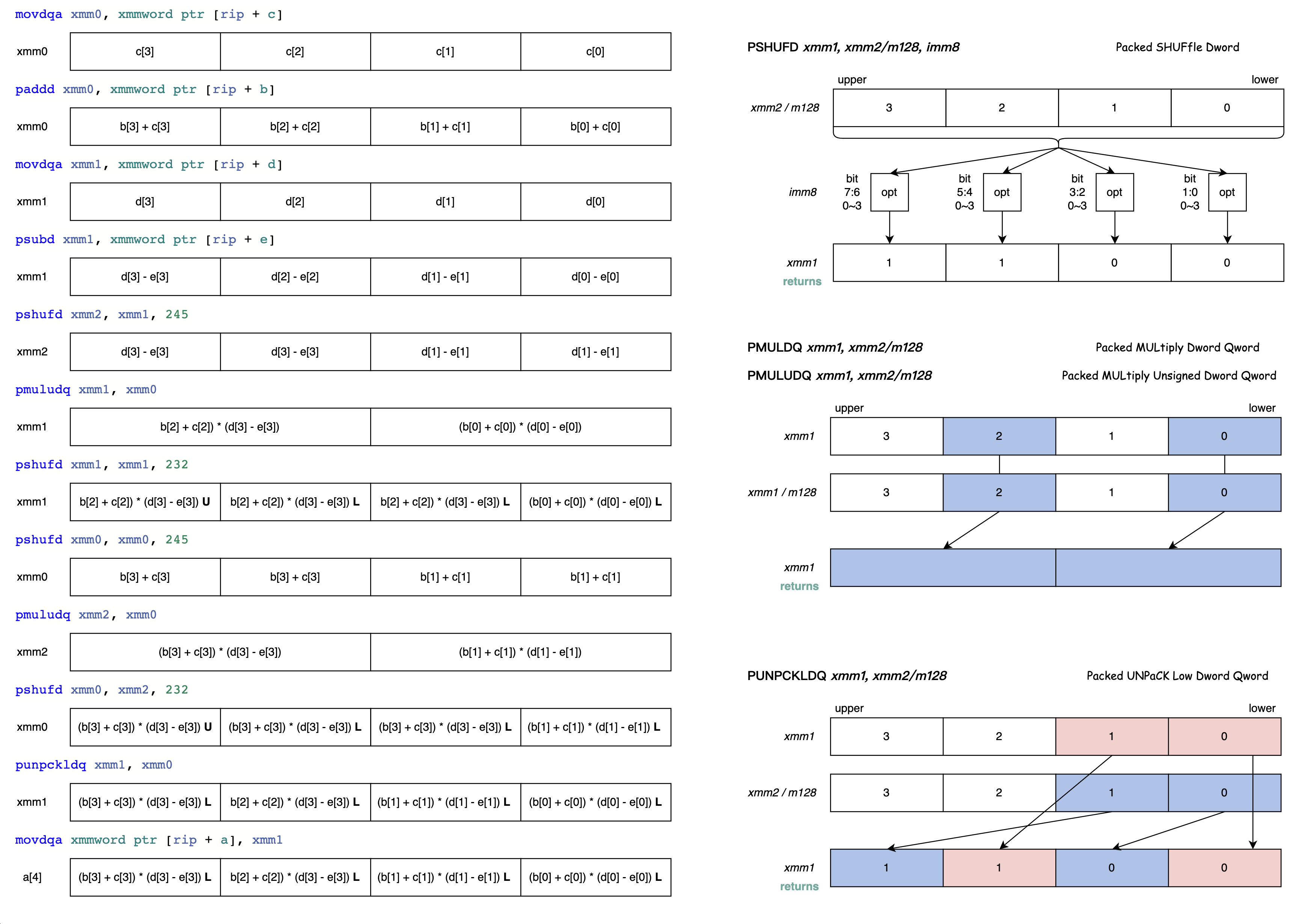
foo(): # @foo() movdqa xmm0, xmmword ptr [rip + c] paddd xmm0, xmmword ptr [rip + b] movdqa xmm1, xmmword ptr [rip + d] psubd xmm1, xmmword ptr [rip + e] pshufd xmm2, xmm1, 245 # xmm2 = xmm1[1,1,3,3] pmuludq xmm1, xmm0 pshufd xmm1, xmm1, 232 # xmm1 = xmm1[0,2,2,3] pshufd xmm0, xmm0, 245 # xmm0 = xmm0[1,1,3,3] pmuludq xmm2, xmm0 pshufd xmm0, xmm2, 232 # xmm0 = xmm2[0,2,2,3] punpckldq xmm1, xmm0 # xmm1 = xmm1[0],xmm0[0],xmm1[1],xmm0[1] movdqa xmmword ptr [rip + a], xmm1 ret为了方便理解 SLP 向量化后的汇编代码,下图详细说明了每一条汇编指令单步执行的效果:
Details of LLVM SLP implementation
本节剖析 SLP Vectorizer 在 LLVM 中的代码实现。
注:在上一节 “Overview of the bottom-up SLP algorithm” 中,称从种子指令开始沿着 use-def 链自底向上构建的数据结构为图;在本节 “Details of LLVM SLP implementation” 中 ,为了保持与 LLVM 代码命名的一致,则称之为树,但实际上构建出的数据结构并不是树而是有向无环图。
// In: Function before SLPVectorizer
// Out: Function after SLPVectorizer
runOnFunction(Function) {
// Scan the blocks in the function in post order.
for BasicBlock in post_order(Function):
Stores, GEPs = collectSeedInstructions(BasicBlock)
// Vectorize trees that end at stores.
if not Stores.empty():
vectorizeStoreChains(Stores)
// Vectorize trees that end at reductions.
vectorizeChainsInBlock(BasicBlock)
// Vectorize the index computations of getelementptr instructions. This
// is primarily intended to catch gather-like idioms ending at
// non-consecutive loads.
if not GEPs.empty():
vectorizeGEPIndices(GEPs)
}
SLPVectorizer Pass 是一个 FunctionPass,其核心入口函数就是 SLPVectorizer::runOnFunction()。SLPVectorizer::runOnFunction() 会后序遍历当前函数的所有基本块,对于每个基本块,首先调用 collectSeedInstructions() 收集种子指令集合 seed instructions,然后依次调用 vectorizeStoreChains(),vectorizeChainsInBlock(),vectorizeGEPIndices() 尝试向量化。
collectSeedInstructions
// Visit the store and getelementptr instructions in BB and organize them in
// Stores and GEPs according to the underlying objects of their pointer operands.
// In: BasicBlock
// Out: Stores, GEPs
collectSeedInstructions(BasicBlock) {
Stores = empty map
GEPs = empty map
for Instruction in BasicBlock:
// Ignore store instructions that are atomic or volatile or
// have a pointer operand that doesn't point to a scalar type.
if Instruction isa StoreInst:
if (not StoreInst.isAtomic() and not StoreInst.isVolatile()) and
isValidVectorElementType(StoreInst.getValueOperand().getType()):
Stores[GetUnderlyingObject(StoreInst.getPointerOperand())].append(StoreInst)
// Ignore getelementptr instructions that have more than one index, a
// constant index, or a pointer operand that doesn't point to a scalar
// type.
if instruction isa GetElementPtrInst:
if (not GetElementPtrInst.getNumIndices() > 1) and
(not GetElementPtrInst.idx_begin() isa Constant) and
isValidVectorElementType(GetElementPtrInst.idx_begin().getType()) and
(not GetElementPtrInst.getType().isVectorTy()):
GEPs[GetUnderlyingObject(GetElementPtrInst.getPointerOperand())].append(GetElementPtrInst)
return Stores, GEPs
}
Seed instructions 是两种类型的指令:StoreInst 和 GetElementPtrInst。
StoreInst:只关心非 atomic 非 volatile 且 value operand 是可向量化的类型的StoreInst。其中,可向量化的类型包括 integer type, floating point type 和 pointer type。%ptr = alloca i32 store atomic i32 0, i32* %ptr seq_cst ; not seed store volatile i32 0, i32* %ptr ; not seed store atomic volatile i32 0, i32* %ptr unordered ; not seed %i = alloca <4 x i32> store <4 x i32> <i32 1, i32 2, i32 3, i32 4>, <4 x i32>* %i ; not seed @a = global [4 x i32] zeroinitializer store i32 0, i32* getelementptr inbounds ([4 x i32], [4 x i32]* @a, i32 0, i64 0) ; seedGetElementPtrInst:如果GetElementPtrInst只有一个 index,该 index 不是 contant,该 index 的类型是可向量化的(即该 index 的类型为 integer type, floating point type 或 pointer type),并且GetElementPtrInst自身的类型不是向量类型,那么会收集该GetElementPtrInst作为 seed instruction。%struct.X = type { i32*, i32* } %x = alloca %struct.X %q2 = getelementptr inbounds %struct.X, %struct.X* %x, i32 0, i32 1 ; not seed %ptr = getelementptr inbounds i32*, i32** %q2, i32 %offset ; seed
vectorizeStoreChains
vectorizeStoreChains(StoreSeeds) {
Changed = false
// Attempt to vectorize each of the store-groups.
for _, Stores in StoreSeeds:
// We may run into multiple chains that merge into a single chain. We mark the
// stores that we vectorized so that we don't visit the same store twice.
VectorizedStores = empty list
// Find all of the pairs of stores that follow each other.
Tails, Heads, ConsecutiveChain = findConsecutiveStoreChain(Stores)
// For stores that start but don't end a link in the chain:
for Inst in Heads:
if Tails.count(Inst):
continue
// We found a storeinst that starts a chain. Now follow the chain and try
// to vectorize it.
Operands = empty list
// Collect the chain into a list.
while (Inst in Tails or Inst in Heads) and (Inst not in VectorizedStores):
Operands.append(Inst)
// Move to the next value in the chain.
Inst = ConsecutiveChain[Inst]
// Try different vectorization factors for store chains
for Size from getMaxVecRegSize() to getMinVecRegSize() by dividing Size by 2:
if (vectorizeStoreChain(Operands, Size)):
VectorizedStores.extend(Operands)
Changed |= true
break
// Return vectorized or not
return Changed
}
vectorizeStoreChains 函数的输入参数是 StoreSeeds 即 StoreInst 类型的 seed instructions,返回值 Changed 表示是否成功进行了向量化操作。
首先,调用
findConsecutiveStoreChain函数找到访问相邻内存地址的StoreInst对,保存在Heads、Tails和ConsecutiveChain中。然后,根据
Heads、Tails和ConsecutiveChain,找到由多对访问相邻内存地址的 StoreInst 组成的 StoreChain。最后,代码尝试使用不同的向量化因子 (vectorization factor) 对 StoreChain 调用
vectorizeStoreChain()函数进行向量化。
findConsecutiveStoreChain
findConsecutiveStoreChain(Stores) {
Heads = Tails = empty list
ConsecutiveChain = empty map
// Do a quadratic search on all of the given stores and find
// all of the pairs of stores that follow each other.
for Index, CurrStore in enumerate(Stores):
// If a store has multiple consecutive store candidates, search Stores
// array according to the sequence: from i+1 to e, then from i-1 to 0.
// This is because usually pairing with immediate succeeding or preceding
// candidate create the best chance to find slp vectorization opportunity.
SearchQueue = Stores[Index+1:] + Stores[:Index][::-1]
for NextStore in SearchQueue:
// If the memory operations of pointer operand of CurrStore and
// pointer operand of NextStore are consecutive.
// pointer operand of CurrStore is the lower address,
// pointer operand of NextStore is the higher address.
if isConsecutiveAccess(CurrStore, NextStore):
Tails.insert(NextStore)
Heads.insert(CurrStore)
ConsecutiveChain[CurrStore] = NextStore
break
return Tails, Heads, ConsecutiveChain
}
函数 findConsecutiveStoreChain() 接收一组 StoreInst 作为输入,找到访问相邻内存地址的 StoreInst 对(即两个 StoreInst 的 pointer operand 是相邻的内存地址),将这些访问相邻内存地址的 StoreInst 对的信息存储在 Heads、Tails 和 ConsecutiveChain 这三个数据结构中并返回。
初始化三个数据结构
Heads、Tails和ConsecutiveChain,用于存储访问相邻内存地址的 StoreInst 对的信息。对于输入 Stores 集合中的每一个
StoreInst,构建一个搜索队列SearchQueue,该队列由 Stores 中当前StoreInst之后的所有StoreInst和 Stores 中当前StoreInst之前的所有StoreInst(倒序)组成。对于输入 Stores 集合中的每一个
StoreInst,遍历搜索队列SearchQueue中的每一个StoreInst,调用isConsecutiveAccess函数判断它们的 pointer operand 是否为相邻的内存地址。关于isConsecutiveAccess函数的实现有时间可以深入分析,是基于 Scalar Evolution (SCEV) 实现的。如果这两个
StoreInst访问的是相邻内存地址,将它们分别添加到Heads和Tails集合中,并将它们的相邻关系记录到ConsecutiveChain映射中。
vectorizeStoreChain
vectorizeStoreChain(Chain, VecRegSize) {
Changed = false;
// The vectorization factor: the number of lanes in the vector unit
VF = VecRegSize / getVectorElementSize(Chain[0])
// Look for profitable vectorizable trees at all offsets, starting at zero.
i = 0
while i < len(Chain) - VF + 1:
ChainSlice = Chain[i:i+VF]
buildTree(ChainSlice)
buildExternalUses()
if (getTreeCost() < -SLPCostThreshold):
vectorizeTree()
i += VF -1 // Move to the next bundle.
Changed = true
return Changed
}
函数 vectorizeStoreChain() 的输入参数是 Chain 和 VecRegSize,Chain 保存的是由多对访问相邻内存地址的 StoreInst 组成的 StoreChain 列表,VecRegSize 表示向量寄存器的大小,返回值 Changed 表示是否对 StoreChain 成功向量化。
函数的核心逻辑如下:
计算向量化因子
VF,向量化因子决定了在执行一个向量指令时可以同时操作的数据元素的数量。遍历
Chain中所有的连续 VF 个StoreInst(记作ChainClice)尝试进行向量化:以ChainClice作为 SLP 树的根节点,调用函数buildTree()尝试构建 SLP 树。在 SLP 图构建完成后,调用函数getTreeCost()估算向量化后的代码在运行时的指令开销与原本的标量指令在运行时的指令开销的差值,如果该差值低于阈值-SLPCostThreshold,则调用vectorizeTree()进行向量化。
buildTree
// In: Insts, i.e. Candidate scalar array for vectorization
// Out: VectorizableTree, i.e. SLP tree/graph of grouped scalars
buildTree_rec(Insts) {
// Check the termination conditions
if not vectorizable(Insts):
// Gather the instructions, append new node to tree and stop growing tree
VectorizableTree.addNode(/*ScalarInsts*/Insts, /*State*/Gather)
return
// Recurisivly create node and add to tree following use-def chain
switch(Insts[0].getOpcode()) {
case Instruction::Load: {
// Check if any load in the bundle is atomic or volatile
if any(LoadInst.isAtomic() or LoadInst.isVolatile() for LoadInst in Insts):
VectorizableTree.addNode(/*ScalarInsts*/Insts, /*State*/Gather)
return
// Check if the loads are consecutive
for CurrLoad, NextLoad in pairwise(Insts):
if not isConsecutiveAccess(CurrLoad, NextLoad):
VectorizableTree.addNode(/*ScalarInsts*/Insts, /*State*/Gather)
return
// Create Vectorized node and add to Graph
VectorizableTree.addNode(/*ScalarInsts*/Insts, /*State*/Vectorize)
return
}
case Instruction::Store: {
// Check if the stores are consecutive
for CurrStore, NextStore in pairwise(Insts):
if not isConsecutiveAccess(CurrStore, NextStore):
VectorizableTree.addNode(/*ScalarInsts*/Insts, /*State*/Gather)
return
VectorizableTree.addNode(/*ScalarInsts*/Insts, /*State*/Vectorize)
Operands = [StoreInst.getValueOperand() for StoreInst in Insts]
buildTree_rec(Operands)
return
}
case Instruction::BinaryOperator: {
VectorizableTree.addNode(/*ScalarInsts*/Insts, /*State*/Vectorize)
LeftOperands = [BinOp.getOperand(0) for BinOp in Insts]
RightOperands = [BinOp.getOperand(1) for BinOp in Insts]
buildTree_rec(LeftOperands)
buildTree_rec(RightOperands)
return
}
// Handle all kinds of Instructions
}
buildTree_rec() 函数是一个递归函数,根据给定的一组标量指令来构建相应的 SLP 树。该函数最初以一组种子指令作为输入进行调用。
首先,检查是否满足递归终止条件,即判断输入的这组标量指令是否可以进行向量化。
如果是可向量化的,那么会将这组标量指令作为一个节点添加至 SLP 树中。
最后,沿着 use-def 链,对输入指令的所有操作数调用自身,尝试尽可能向量化更多的指令。
buildTree_rec() 函数的输出 VectorizableTree 的每个节点代表一个候选向量化的标量指令组。
buildTree_rec() 函数对递归终止条件的判断,就是判断一组标量指令是否可向量化,主要是判断是否满足以下几个条件:i) scalars, ii) isomorphic, iii) unique, iv) all in the same basic block, v) not yet in the SLP graph, and vi) schedulable 。
判断 i) scalars, ii) isomorphic, iii) unique, iv) all in the same basic block, v) not yet in the SLP graph 的实现比较简单、容易理解,这里不再介绍。
这里着重分析下判断是否 schedulable 的实现:
Schedulable 的基本单位是 BasicBlock,每个 BasicBlock 都对应一个 ScheduleRegion,ScheduleRegion 是包含当前 BasicBlock 中候选向量化的标量指令的最小连续指令序列 [ScheduleStart, ScheduleEnd)
给定一候选向量化的标量指令组 Bundle,扩展 Bundle 所在 BasicBlock 对应的 ScheduleRegion,使得 ScheduleRegion 包含候选向量化的标量指令组 Bundle
如果候选向量化的标量指令 Bundle 没有任何依赖,或者其依赖都是 schedulable,那么 Bundle 就是 schedulable。
因此需要计算候选向量化的标量指令组 Bundle 的依赖。Bundle 的依赖就是 Bundle 中每一条指令的依赖的集合。依赖分为 def-use chain dependencies 和 memory dependencies:
def-use chain dependencies: 对于候选向量化的标量指令组 Bundle 中的每一条指令 BundleMember,根据 def-use chain 找到其 user instruction(s),如果 user instruction(s) 也在当前 ScheduleRegion 中,则将该 user instruction(s) 作为 Bundle 的 def-use chain dependency(ies)。
memory dependencies: 对于候选向量化的标量指令组 Bundle 中的每一条指令 BundleMember,如果 ScheduleRegion 中存在满足如下条件的指令 MI,那么就将该 MI 指令作为 Bundle 的 memory dependency。
MI 指令在 ScheduleRegion 的位置位于 BundleMember 指令之后。
MI 指令与 BundleMember 指令可能访问同一内存位置(基于别名分析 AliasAnalysis),并且 MI 指令与 BundleMember 指令中至少有一个会对该内存位置进行写操作。
因此判断候选向量化的标量指令组 Bundle 是否 schedulable:首先通过 WorkList 算法自顶向下计算 Bundle 的依赖以及间接依赖(Bundle 依赖的依赖,依赖的依赖的依赖,etc),然后再自底向上计算间接依赖是否 schedulable,直接依赖是否 schedulable,最后得出 Bundle 是否 schedulable。
buildExternalUses
// Builds external uses of the vectorized scalars, i.e. the list of
// vectorized scalars to be extracted, their lanes and their scalar users.
// In: VectorizableTree, i.e. SLP tree/graph of grouped scalars.
// Out: ExternalUses, i.e. a list of values that need to extracted out of the tree.
// This list holds pairs of (Internal Scalar : External User).
buildExternalUses() {
for Node in VectorizableTree:
// No need to handle users of gathered values.
if Node.State == Gather:
continue
for Lane, ScalarInst in enumerate(Node.ScalarInsts):
for UserInst in ScalarInst.users():
if not UserInst in VectorizableTree:
ExternalUses.append({ScalarInst, UserInst, Lane})
}
buildExternalUses() 函数的输入为 VectorizableTree 即 buildTree() 函数创建的 SLP 树。该函数会遍历 VectorizableTree 中的每个节点,跳过 State 为 Gather 的节点,只处理 State 为 Vectorize 的节点,对于节点的候选向量化的标量指令组中的每一条指令,检查其使用点(指令),如果使用指令不在 VectorizableTree 中,则将元组 (ScalarInst, UserInst, Lane) 添加到 ExternalUses 列表中。
getTreeCost
// Returns the vectorization cost of the SLP tree.
// A negative number means that this is profitable.
// In: 1) VectorizableTree, i.e. SLP tree/graph of grouped scalars.
// 2) ExternalUses, i.e. list of values that need to extracted out of the tree.
// Out: the vectorization cost of the SLP tree.
getTreeCost() {
Size = VectorizableTree[0].ScalarInsts.size()
// Calculate the cost of gathering/vectorizing nodes in VectorizableTree.
Cost1 = 0
for Node in VectorizableTree:
ScalarType = Node.ScalarInsts[0].getType()
VectorType = createVectorType(ScalarType, Size)
if Node.State == Gather:
if allContant(Node.ScalarInsts): // all of the values are constants
cost1 += 0
else if isSplat(Node.ScalarInsts): // all of the values are identical
cost1 += TargetTransformInfo.getShuffleCost(
ShuffleKind::SK_Broadcast, VectorType, 0)
else:
for Lane in range(0, Size):
Cost1 += TargetTransformInfo.getVectorInstrCost(
Instruction::InsertElement, VectorType, Lane)
if Node.State == Vectorize:
Opcode = Node.ScalarInsts[0].getOpcode()
ScalarCost = Size * TargetTransformInfo.getInstrCost(Opcode, ScalarType)
VectorCost = TargetTransformInfo.getInstrCost(Opcode, VectorType)
Cost1 += VectorCost - ScalarCost
// Calculate the cost of extracting the values for external uses.
Cost2 = 0
for ScalarInst, UserInst, Lane in ExternalUses:
VectorType = createVectorType(ScalarInst.getType(), Size)
Cost2 += TargetTransformInfo.getVectorInstrCost(
Instruction::ExtractElement, VectorType, Lane)
// Calculate the cost incurred by unwanted spills and fills, caused by
// holding live values over call sites.
Cost3 = 0
LiveValues = set()
// Walk from the bottom of the tree to the top, tracking which values are
// live. When we see a call instruction that is not part of our tree,
// query TargetTransformInfo to see if there is a cost to keeping values
// live over it (for example, if spills and fills are required).
for PrevNode, CurrNode in pairwise(VectorizableTree):
PrevInst = PrevNode.ScalarInsts[0]
CurrInst = CurrNode.ScalarInsts[0]
LiveValues.erase(PrevInst);
for Inst in PrevInst.operands():
if Inst in VectorizableTree:
LiveValues.insert(Inst)
for Inst in range(PrevInst, CurrInst):
if Inst isa CallInst:
V = [createVectorType(LiveInst.getType(), Size) for LiveInst in LiveValues]
Cost3 += TargetTransformInfo.getCostOfKeepingLiveOverCall(V)
return Cost1 + Cost2 + Cost3
}
函数 getTreeCost(),基于编译器的 target-specific cost model(LLVM 中 TargetTransformInfo 类提供了 target-specific cost model 相关接口),通过估算 SLP 树向量化后的代码在运行时的指令开销与原本的标量指令在运行时的指令开销的差值,判断将 SLP 树向量化后是否有性能收益。该函数将考虑了以下几个方面的开销:
Cost1 :将
VectorizableTree中节点的标量指令转换为向量指令带来的开销(可能为负)。Cost2:对于
VectorizableTree中的节点,如果被向量化的标量指令存在VectorizableTree之外的使用点,那么向量化时需要生成额外的指令ExtractElementInst将其从向量中提取出来用于VectorizableTree之外的使用点。需要考虑额外生成的指令ExtractElementInst带来的开销。Cost3:如果经向量化后某个保存在向量寄存器中的值的生命周期会跨越函数调用指令,那么可能需要额外的 spill 和 refill 操作,这也会带来一定的开销。
vectorizeTree
// Vectorize the tree, replacing the groups of scalar instructions with their equivalent vector instructions
// In: 1) VectorizableTree, i.e. SLP tree/graph of grouped scalars.
// 2) ExternalUses, i.e. list of values that need to extracted out of the tree.
vectorizeTree() {
/* All blocks must be scheduled before vectorizeTree_rec() */
/* Performs scheduling for all ScheduleRegions. */
vectorizeTree_rec(VectorizableTree[0])
for ScalarInst, UserInst, Lane in ExternalUses:
VectorizedInst = getVectorizedInst(ScalarInst)
ExtractElementInst = CreateExtractElementInst(VectorizedInst, Lane)
UserInst.replaceUsesOfWith(Scalar, ExtractElementInst);
for Group in VectorizableTree:
for Lane, ScalarInst in enumerate(Group.ScalarInsts):
eraseInstruction(ScalarInst)
}
在函数
buildTree()中我们提到:判断一组标量指令可以进行向量化的其中一个条件就是 schedulable。Schedulable 的基本单位是 BasicBlock,每个 BasicBlock 都对应一个 ScheduleRegion,ScheduleRegion 是包含当前 BasicBlock 中候选向量化的标量指令的最小连续指令序列 [ScheduleStart, ScheduleEnd)。对所有的 ScheduleRegion 真正进行调度是在函数vectorizeTree()中,调度是指对 ScheduleRegion 中的指令进行重新排序。在 “case study” 一节会通过例子来详细说明如何进行调度。在调度完成后,会以
VectorizableTree的根节点为参数调用vectorizeTree_rec()函数,此函数会从根节点遍历整个VectorizableTree递归地为标量指令组生成相应的向量指令。然后,遍历
ExternalUses列表中的每个元组(ScalarInst, UserInst, Lane)。其中,ScalarInst是被替换为向量指令的标量指令,UserInst是不在VectorizableTree中的使用该标量指令的指令。使用CreateExtractElementInst()函数新增ExtractElementInst指令,用于从向量指令中提取指定的位置Lane的元素,然后将UserInst中所有使用到Scalar的地方替换为ExtractElementInst从向量中提取出的元素。最后,删除
VectorizableTree中所有被向量化的标量指令组中的标量指令。
// In: Node, i.e. grouped candidate scalars for vectorization
// Out: Vectorized instruction of grouped candidate scalars
vectorizeTree_rec(Node) {
Size = Node.ScalarInsts.size()
// We need to gather this sequence instead of vectorize
if Node.state == Gather:
InsertElementInst = UndefValue
for Lane, ScalarInst in enumerate(Node.ScalarInsts):
InsertElementInst = CreateInsertElement(InsertElementInst, ScalarInst, Lane)
return InsertElementInst
// Here Node.state must be Vectorize, vectorize it
Opcode = Node.ScalarInsts[0].getOpcode()
setInstructionsInsertPointAfterBundle(Group.ScalarInsts)
switch(Opcode) {
case Instruction::BinaryOperator: {
LeftOperands = [BinOp.getOperand(0) for BinOp in Node.ScalarInsts]
RightOperands = [BinOp.getOperand(1) for BinOp in Node.ScalarInsts]
LHS = vectorizeTree_rec(LeftOperands)
RHS = vectorizeTree_rec(RightOperands)
Node.VectorizedInst = CreateBinaryOperator(BinOp.getOpcode(), LHS, RHS)
return Node.VectorizedInst
}
case Instruction::Load: {
LoadInst = Node.ScalarInsts[0]
VecPtrTy = createVectorType(LoadInst.getPointerOperand().getType(), Size)
VecPtr = CreateBitCast(LoadInst.getPointerOperand(), VecPtrTy)
Node.VectorizedInst = CreateLoadInst(VecPtr)
return Node.VectorizedInst
}
case Instruction::Store: {
StoreInst = Node.ScalarInsts[0]
ValueOperands = [StoreInst.getValueOperand() for StoreInst in Group.ScalarInsts]
VecValue = vectorizeTree_rec(ValueOperands)
VecPtrTy = createVectorType(StoreInst.getPointerOperand().getType(), Size)
VecPtr = CreateBitCast(StoreInst.getPointerOperand(), VecPtrTy)
VectorStoreInst = CreateStoreInst(VecValue, VecPtr)
Node.VectorizedInst = VectorStoreInst
return VectorLoadInst
}
// handle all kinds of Instructions
}
}
vectorizeTree_rec() 函数是一个递归函数,为给定的一组候选向量化的标量指令生成其对应的向量化指令。
首先处理需要 Gather 的一组标量指令,创建一个
InsertElementInst的初始值为UndefValue。然后,通过循环遍历Node.ScalarInsts中的每个标量指令,并使用CreateInsertElement()函数将它们插入到InsertElementInst中的相应位置。接下来处理需要向量化的一组标量指令,这里以
BinaryOperator为例进行说明:分别获取所有标量指令的左操作数和右操作数,调用vectorizeTree_rec()函数对左操作数和右操作数进行向量化处理。然后以向量化后的左操作数和向量化后的右操作数作为操作数创建一个向量化的BinaryOperator。
vectorizeChainsInBlock
vectorizeChainsInBlock(BB) {
Changed = false
// Try to vectorize the incoming values from the PHIs.
HaveVectorizedPhiNodes = true
VisitedInstrs = empty set
while HaveVectorizedPhiNodes:
Incoming = [PHINode for Inst in BB if Inst isa PHINode and Inst not in VisitedInstrs]
sort PHINode in Incoming by type
// Try to vectorize elements base on their type.
i, e = 0, len(Incoming)
while i < e:
// Look for the next elements with the same type.
SameType = i
while SameType < e and
Incoming[i].getType() == Incoming[SameType].getType():
VisitedInstrs.insert(Incoming[SameType])
++SameType
tryToVectorizeList(Incoming[i:SameType])
RestartLoop:
for Inst in BB:
// We may go through BB multiple times so skip the one we have checked.
if Inst in VisitedInstrs:
continue
VisitedInstrs.add(Inst)
// Try to vectorize reductions that use PHINodes.
if Instr isa PHINode:
// Try and get a reduction value from a PHINode.
Rdx = getReductionValue(PHINode)
if not Rdx isa BinaryOperator:
continue
// Try to match and vectorize a horizontal reduction.
if tryReduceHorizontalReduction(PHINode, Rdx):
Changed = true
goto RestartLoop
// If it is not a horizontal reduction or vectorization is not possible
// or not effective, try to vectorize the operands.
Op = Rdx.getOperand(1) if Rdx.getOperand(0) == PHINode else Rdx.getOperand(0)
if Op isa BinaryOperator and tryToVectorizeList([Op.getOperand(0), Op.getOperand(1)]):
changed= true
goto RestartLoop
continue
// Try to vectorize horizontal reductions feeding into a store
if Inst isa StoreInst and StoreInst.getValueOperand() isa BinaryOperator:
BinOp = StoreInst.getValueOperand()
if tryReduceHorizontalReduction(nullptr, BinOp) or
tryToVectorizeList([BinOp.getOperand(0), BinOp.getOperand(1)]):
goto RestartLoop
// Try to vectorize horizontal reductions feeding into a return.
if Inst isa ReturnInst and ReturnInst.getOperand(0) isa BinaryOperator:
BinOp = ReturnInst.getOperand(0)
if tryReduceHorizontalReduction(nullptr, BinOp) or
tryToVectorizeList([BinOp.getOperand(0), BinOp.getOperand(1)]):
goto RestartLoop
// Try to vectorize trees that start at compare instructions.
// Try to vectorize trees that start at insertelement instructions.
// Try to vectorize trees that start at insertvalue instructions feeding into
// a store.
return Changed
}
vectorizeChainsInBlock() 函数的目标是在给定的基本块中尝试对指令进行向量化处理。
首先,尝试对当前基本块中同类型的
PHINode进行向量化。一旦成功对PHINode向量化,则会重新收集当前基本块中的PHINode,再次尝试对PHINode向量化,直至没有新的可向量的PHINode为止。然后,尝试对 reduction value 进行向量化。调用
getReductionValue()函数尝试从PHINode中获取 reduction value,当前只支持对BinaryOperator类型的 reduction value,调用tryReduceHorizontalReduction()函数尝试向量化。之后,尝试对
StoreInst和ReturnInst的BinaryOperator类型的操作数尝试向量化。先tryReduceHorizontalReduction()函数尝试进行向量化,如果tryReduceHorizontalReduction()未能成功向量化,则调用tryToVectorizeList()再次尝试向量化。接下来,会尝试对
CmpInst,InsertElementInst,InsertValueInst的操作数进行向量化,略。一旦上述某一步向量化成功,则会重新遍历当前基本块的指令尝试进行向量化。
tryToVectorizeList
由于篇幅原因,这里不再给出 tryToVectorizeList() 的伪代码,tryToVectorizeList() 的实现与 vectorizeStoreChain() 基本上是一致的:以给定的参数作为 SLP 树的根节点,调用函数 buildTree 尝试构建 SLP 树。在 SLP 图构建完成后,调用函数 getTreeCost() 估算向量化后的代码在运行时的指令开销与原本的标量指令在运行时的指令开销的差值,如果该差值低于阈值 -SLPCostThreshold,则调用 vectorizeTree() 进行向量化。
getReductionValue
// Try and get a reduction value from a phi node.
// Given a phi node, consider possible reductions if they come from
// the same BasicBlock as the phi node or a containing loop latch.
getReductionValue(PHINode) {
ParentBB = PHINode.getParent()
// Return the incoming value if it comes from the same BB as the phi node.
ReductionValue =
PHINode.getIncomingValue(0) if getIncomingValue(0) == ParentBB
else (PHINode.getIncomingValue(1) if getIncomingValue(1) == ParentBB
else nullptr)
if ReductionValue and
DominatorTree.dominates(ParentBB, ReductionValue.getParent()):
return ReductionValue
// Otherwise, check whether we have a loop latch to look at.
Loop = LoopInfo.getLoopFor(ParentBB)
if not Loop:
return nullptr
BBLatch = Loop.getLoopLatch()
if not BBLatch:
return nullptr
// There is a loop latch, return the incoming value if it comes from
// that. This reduction pattern occasionally turns up.
ReductionValue =
PHINode.getIncomingValue(0) if getIncomingValue(0) == BBLatch
else (PHINode.getIncomingValue(1) if getIncomingValue(1) == BBLatch
else nullptr)
if ReductionValue and
DominatorTree.dominates(PHINode.getParent(), ReductionValue.getParent()):
return ReductionValue
return nullptr
}
函数 getReductionValue() 用于根据给定的 PHINode 寻找 reduction value,考虑两种情况:
reduction value 来自与
PHINode相同的基本块以 llvm/test/Transforms/SLPVectorizer/X86/reduction2.ll 为例:
define double @foo(double* nocapture %D) { br label %1 ; <label>:1 ; preds = %1, %0 %i.02 = phi i32 [ 0, %0 ], [ %10, %1 ] %sum.01 = phi double [ 0.000000e+00, %0 ], [ %9, %1 ] ... %9 = fadd double %sum.01, %8 %10 = add nsw i32 %i.02, 1 %exitcond = icmp eq i32 %10, 100 br i1 %exitcond, label %11, label %1 ; <label>:11 ; preds = %1 ret double %9 }以
%sum.01 = phi double [ 0.000000e+00, %0 ], [ %9, %1 ]作为输入,函数getReductionValue()返回%9 = fadd double %sum.01, %8。reduction value 包含该
PHINode的循环的 latch blocklatch block 是什么?见 https://llvm.org/docs/LoopTerminology.html#terminology
以如下修改自 llvm/test/Transforms/SLPVectorizer/X86/horizontal.ll 的 IR 为例:
define i32 @add_red(float* %A, i32 %n) #0 { entry: %cmp31 = icmp sgt i32 %n, 0 br i1 %cmp31, label %for.body.lr.ph, label %for.end for.body.lr.ph: ; preds = %entry %0 = sext i32 %n to i64 br label %for.body for.body: ; preds = %for.latch, %for.body.lr.ph %i.033 = phi i64 [ 0, %for.body.lr.ph ], [ %inc, %for.latch ] %sum.032 = phi float [ 0.000000e+00, %for.body.lr.ph ], [ %add17, %for.latch ] br label %for.latch for.latch: ; preds = %for.body %mul = shl nsw i64 %i.033, 2 %arrayidx = getelementptr inbounds float, float* %A, i64 %mul %1 = load float, float* %arrayidx, align 4 %mul2 = fmul float %1, 7.000000e+00 %add28 = or i64 %mul, 1 %arrayidx4 = getelementptr inbounds float, float* %A, i64 %add28 %2 = load float, float* %arrayidx4, align 4 %mul5 = fmul float %2, 7.000000e+00 %add6 = fadd fast float %mul2, %mul5 %add829 = or i64 %mul, 2 %arrayidx9 = getelementptr inbounds float, float* %A, i64 %add829 %3 = load float, float* %arrayidx9, align 4 %mul10 = fmul float %3, 7.000000e+00 %add11 = fadd fast float %add6, %mul10 %add1330 = or i64 %mul, 3 %arrayidx14 = getelementptr inbounds float, float* %A, i64 %add1330 %4 = load float, float* %arrayidx14, align 4 %mul15 = fmul float %4, 7.000000e+00 %add16 = fadd fast float %add11, %mul15 %add17 = fadd fast float %sum.032, %add16 %inc = add nsw i64 %i.033, 1 %exitcond = icmp eq i64 %inc, %0 br i1 %exitcond, label %for.cond.for.end_crit_edge, label %for.body for.cond.for.end_crit_edge: ; preds = %for.latch %phitmp = fptosi float %add17 to i32 br label %for.end for.end: ; preds = %for.cond.for.end_crit_edge, %entry %sum.0.lcssa = phi i32 [ %phitmp, %for.cond.for.end_crit_edge ], [ 0, %entry ] ret i32 %sum.0.lcssa }以
%sum.032 = phi float [ 0.000000e+00, %for.body.lr.ph ], [ %add17, %for.latch ]作为输入,函数getReductionValue()返回%add17 = fadd fast float %sum.032, %add16。其中,基本块
for.body.lr.ph是 Loop 的 predecessor 和 preheader,基本块for.body是 Loop 的 header,基本块for.latch是 Loop 的 latch 和 exiting block,基本块for.cond.for.end_crit_edge是 Loop 的 exit block。
tryReduceHorizontalReduction
由于篇幅原因,这里不再给出 tryReduceHorizontalReduction() 的伪代码,简单描述下 tryReduceHorizontalReduction() 的流程。
tryReduceHorizontalReduction() 的输入是 PHINode 和getReductionValue(PHINode) 得到的 reduction value,首先调用 matchAssociativeReduction() 根据 reduction value 找到 reduction tree,然后调用 trytoReduce() 向量化 reduction tree。trytoReduce() 的实现也是先调用函数 buildTree() 尝试构建 SLP 树。在 SLP 树构建完成后,调用函数 getTreeCost() 和 getReductionCost() 估算向量化后的代码在运行时的指令开销与原本的标量指令在运行时的指令开销的差值,如果该差值低于阈值 -SLPCostThreshold,则调用 vectorizeTree() 进行向量化。
可以结合 “case study” 一节理解 tryReduceHorizontalReduction() 的流程。
vectorizeGEPIndices
vectorizeGEPIndices(GEPSeeds) {
Changed = false
// Vectorize the index computations of the getelementptr instructions.
for _, GEPs in GEPSeeds:
// Initialize a set a candidate getelementptrs.
Candidates = set(GEPs)
// Some of the candidates may have already been vectorized after we
// initially collected them.
Candidates.remove_if(
[](GetElementPtrInst) { return isDeleted(GetElementPtrInst); });
// Remove from the set of candidates all pairs of getelementptrs with
// constant differences. Such getelementptrs are likely not good
// candidates for vectorization in a bottom-up phase since one can be
// computed from the other. We also ensure all candidate getelementptr
// indices are unique.
for GEPI, GEPJ in pairwise(GEPs):
if not GEPI in Candidates:
continue
SCEVI = ScalarEvolution.getSCEV(GEPI)
SCEVJ = ScalarEvolution.getSCEV(GEPJ)
if ScalarEvolution.getMinusSCEV(SCEVI, SCEVJ) isa SCEVConstant:
Candidates.remove(GEPI)
Candidates.remove(GEPJ)
else if GEPI.idx_begin() == GEPJ.idx_begin():
Candidates.remove(GEPJ)
// Add the single, non-constant index of each candidate to the bundle. We
// ensured the indices met these constraints when we originally collected
// the getelementptrs.
Bundle = empty list
for GEP in Candidates:
GEPIdx = GEP->idx_begin()->get()
assert((GEP.getNumIndices() == 1) and (GEPIdx isa Constant))
Bundle.append(GEPIdx)
// Try and vectorize the indices. We are currently only interested in
// gather-like cases of the form:
//
// ... = g[a[0] - b[0]] + g[a[1] - b[1]] + ...
//
// where the loads of "a", the loads of "b", and the subtractions can be
// performed in parallel. It's likely that detecting this pattern in a
// bottom-up phase will be simpler and less costly than building a
// full-blown top-down phase beginning at the consecutive loads.
Changed |= tryToVectorizeList(Bundle)
// Return vectorized or not
return Changed;
}
vectorizeStoreChains() 函数的输入参数是 GEPSeeds 即 GetElementPtrInst 类型的 seed instructions,返回值 Changed 表示是否成功进行了向量化操作。
遍历 GEPSeeds 中的每组 GetElementPtrInst 指令集合 GEPs:
如果在之前的
vectorizeStoreChains和vectorizeChainsInBlock已经将 GEPs 中的某些GetElementPtrInst向量化了,那么从 GEPs 中删除这样的GetElementPtrInst。遍历 GEPs 中的每对相邻的
GetElementPtrInst记作GEPI和GEPJ,如果通过 Scalar Evolution (SCEV) 可以分析出 GEPI 和 GEPJ 所指向的地址有着 constant differences,那么从 GEPs 中删除这样的GetElementPtrInst对。调用
tryToVectorizeList()函数,尝试对GetElementPtrInst进行向量化。
举例说明什么是 GEPI 和 GEPJ 所指向的地址有着 constant differences:
define void @SAXPY_crash(i32* noalias nocapture %x, i32* noalias nocapture %y, i64 %i) {
%1 = add i64 %i, 1
%2 = getelementptr inbounds i32, i32* %x, i64 %1
%3 = getelementptr inbounds i32, i32* %y, i64 %1
%4 = load i32, i32* %3, align 4
%5 = add nsw i32 undef, %4
store i32 %5, i32* %2, align 4
%6 = add i64 %i, 2
%7 = getelementptr inbounds i32, i32* %x, i64 %6
%8 = getelementptr inbounds i32, i32* %y, i64 %6
%9 = load i32, i32* %8, align 4
%10 = add nsw i32 undef, %9
store i32 %10, i32* %7, align 4
ret void
}
经 collectSeedInstructions() 后,%2 = getelementptr inbounds i32, i32* %x, i64 %1 和 %7 = getelementptr inbounds i32, i32* %x, i64 %6 是一组 GetElementPtrInst 类型的 seed instructions,%3 = getelementptr inbounds i32, i32* %y, i64 %1 和 %8 = getelementptr inbounds i32, i32* %y, i64 %6 是一组 GetElementPtrInst 类型的 seed instructions。
%2 = getelementptr inbounds i32, i32* %x, i64 %1 的 SCEV 为 (4 + (4 * %i) + %x),%7 = getelementptr inbounds i32, i32* %x, i64 %6 的 SCEV 为 (8 + (4 * %i) + %x),(4 + (4 * %i) + %x) - (8 + (4 * %i) + %x) = -4 显然是常量,所以这对 GetElementPtrInst 有着 constant differences。
%3 = getelementptr inbounds i32, i32* %y, i64 %1 和 %8 = getelementptr inbounds i32, i32* %y, i64 %6 同理。
Case study
vectorizeStoreChains
以 llvm/test/Transforms/SLPVectorizer/X86/external_user.ll 为例,分析 vectorizeStoreChains() 的流程。

foo()函数的源代码如下所示,对应的 LLVM IR 如上图 (a) 所示。double foo(double * restrict b, double * restrict a, int n, int m) { double r=a[1]; double g=a[0]; double x; for (int i=0; i < 100; i++) { r += 10; g += 10; r *= 4; g *= 4; x = g; // external user! r += 4; g += 4; } b[0] = g; b[1] = r; return x; // must extract here! }SLPVectorizer 会后序遍历
foo()函数的所有基本块,对于每个基本块,首先收集种子指令集合 seed instructions,然后依次调用vectorizeStoreChains(),vectorizeChainsInBlock(),vectorizeGEPIndices()尝试向量化。对于本例,
vectorizeChainsInBlock(),vectorizeGEPIndices()没有任何效果,因此不再分析vectorizeChainsInBlock(),vectorizeGEPIndices()的流程。对于本例,只有基本块
foo.end中存在指令集合 seed instructions,因此不再分析对基本块foo.body和entry尝试向量化的流程。
对于基本块
foo.end,收集到的种子指令集合 seed instructions 为store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7, align 8。因为store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7, align 8是非 atomic 非 volatile 的,并且GetUnderlyingObject(PointerOperand)都是%B,value operand 的类型是 double 是可行量化的。调用函数
findConsecutiveStoreChain从StoreInst类型的 seed instructions 中找到访问相邻内存地址的StoreInst对。store double %add5, double* %B, align 8的 PointerOperand 就是foo()函数的第一个参数%B,store double %add4, double* %arrayidx7, align 8的 pointer operand 则是%arrayidx7 = getelementptr inbounds double, double* %B, i64 1,即%B指针所指向的double类型数组中索引为 1 的元素的地址。显然store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7, align 8这两条StoreInst的 PointerOperand 是相邻的内存地址。从源代码的角度就更好理解了,
store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7, align 8的 PointerOperand 分别对应源代码中的b[0]和b[1],显然他们是相邻的内存地址。以
store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7, align 8组成的 StoreChain 为参数,调用函数vectorizeStoreChain。调用函数
buildTree()来构建 SLP 树。以store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7, align 8组成的 StoreChain 为 SLP 树的根节点,沿着 use-def 链不断添加节点至 SLP 树。 构建出来的 SLP 树如上图 (b) 所示。调用函数
buildExternalUses(),发现 SLP 树中的指令%mul3 = fmul double %add2, 4.000000e+00存在一使用点ret double %mul3不在 SLP 树中。将该ExternalUse记录下来,后续为该ret double %mul3使用点生成ExtractElementInst指令。调用函数
getTreeCost(),估算 SLP 树向量化后的代码在运行时的指令开销与原本的标量指令在运行时的指令开销的差值。具体的每一个 SLP 节点的 cost 已在上图 (b) 中标出。 整个 SLP 树的 cost = (-1 + -2 + -2 + 0 + -2 + 0 + 0 + 0 + -1) + 0 + 0 = -8,其中 ExtractCost 和 SpillCost 都是 0。 ExtractCost = 0 是因为 target-specific cost model 计算ret double %mul3这一ExternalUse的 cost 为 0; SpillCost = 0 则是因此本例中没有需要额外的 spill 和 refill 操作。最后调用函数
vectorizeTree()进行向量化。首先会对所有的 ScheduleRegion 进行调度,即对 ScheduleRegion 中的指令进行重新排序。在上图 (a) 中每个基本块中的 ScheduleRegion 都通过蓝色背景色的方式标识出来了。仔细看图 (c),会注意到在调度之后,基本块
for.end的 ScheduleRegion 中的指令的顺序被改变了。因store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7, align 8会被向量化为一条指令,所以调度会将这两条指令放在一起。for.body和entry基本块的 ScheduleRegion 调度前后没有变化。在调度完成后,递归地为标量指令组生成相应的向量指令。例如为
store double %add5, double* %B, align 8和store double %add4, double* %arrayidx7生成的向量化指令为store <2 x double> %5, <2 x double>* %6, align 8。然后,为
ExternalUses生成ExtractElementInst指令,因为ret double %mul3的操作数%mul3 = fmul double %add2, 4.000000e+00是向量后的%4 = fmul <2 x double> <double 4.000000e+00, double 4.000000e+00>, %5的 Lane 0 元素,所以额外生成%7 = extractelement <2 x double> %4, i32 0并且将ret double %mul3中的%mul替换为%7即ret double %7。最后,删除
VectorizableTree中所有被向量化的标量指令,被删除的标量指令在上图 (d) 中标记为灰色。
vectorizeChainsInBlock
以 llvm/test/Transforms/SLPVectorizer/X86/horizontal.ll 为例,分析 vectorizeChainsInBlock() 是如何向量化 horizontal reduction 的。

add_red()函数的源代码如下所示,对应的 LLVM IR 如上图 (a) 所示。int add_red(float *A, int n) { float sum = 0; for (intptr_t i=0; i < n; ++i) { sum += 7*A[i*4 ] + 7*A[i*4+1] + 7*A[i*4+2] + 7*A[i*4+3]; } return sum; }首先遍历
add_red()函数中的PHINode,调用getReductionValue(PHINode)尝试得到的 reduction value,再调用matchAssociativeReduction()寻找 reduction tree对于
%i.033 = phi i64 [ 0, %for.body.lr.ph ], [ %inc, %for.body ],getReductionValue()返回%inc = add nsw i64 %i.033, 1。调用matchAssociativeReduction()寻找 reduction tree,因为%inc = add nsw i64 %i.033, 1第一个操作数是PHINode,第二个操作数是常数1,找不到以%inc = add nsw i64 %i.033, 1为根结点的 reduction tree。对于
%sum.032 = phi float [ 0.000000e+00, %for.body.lr.ph ], [ %add17, %for.body ],getReductionValue()返回%add17 = fadd fast float %sum.032, %add16。调用matchAssociativeReduction()找到如下所示 reduction tree,reduction tree 的根结点为%add16,有四个叶子结点为%mul2, %mul5, %mul10, %mul15。// A horizontal reduction is a tree of reduction operations // that has operations that can be put into a vector as its leaf. // This tree has "mul" as its reduced values and "+" as its reduction // operations. %mul2 %mul5 %mul2 %mul5 %mul10 %mul15 \ / \ / \ / + \ / \ / %add6 %mul10 + + \ / -- reduction tree --> \ / + \ / %add11 %mul15 + \ / %add16 + %add16
以
%mul2, %mul5, %mul10, %mul15为 SLP 树的根节点,调用函数buildTree()来构建 SLP 树,沿着 use-def 链不断添加节点至 SLP 树。 构建出来的 SLP 树如上图 (c) 所示。调用函数
buildExternalUses(),收集 SLP 树中的指令是否存在 SLP 树之外的使用点ExternalUses。注意,在收集ExternalUses时会忽略 reduction operations。虽然%mul2, %mul5, %mul10, %mul15存在 SLP 树之外的使用点%add6, %add11, %add16,但是%add6, %add11, %add16是 reduction operation,所以不算作ExternalUses。因此,本例是没有ExternalUses的。调用函数
getTreeCost()+getReductionCost(),估算 SLP 树向量化后的代码在运行时的指令开销与原本的标量指令在运行时的指令开销的差值。整个 SLP 树的 cost = VectorizeCost + ExtractCost + SpillCost + ReductionCost = -12,其中 ExtractCost 和 SpillCost 都是 0。
VectorizeCost = -6 + -3 = -9
ExtractCost = 0 是因为本例中没有 ExternalUses
SpillCost = 0 则是因为本例中没有需要额外的 spill 和 refill 操作
ReductionCost = 3 - 6 = -3
reduction 有两种方式:pairwise reduction 或 split reduction,示意图如下:
Pairwise: (v0, v1, v2, v3) ((v0+v1), (v2, v3), undef, undef) Split: (v0, v1, v2, v3) ((v0+v2), (v1+v3), undef, undef)使用 LLVM 的 target-specific cost model 即 TargetTransformInfo 提供的计算 vector reduction cost 的接口
getReductionCost,计算 pairwise reduction cost 为 4,split reduction cost 为 3,由于 split reduction cost 更小,所以在向量化 reduction 时会使用 split reduction 的方式,因此 vector reduction cost 就是 3。计算 scalar reduction cost,未向量化时需要 3 个 + 操作,因此 scalar reduction cost 为 3 * 2 = 6。
调用函数
vectorizeTree()进行向量化。首先会对所有的 ScheduleRegion 进行调度,即对 ScheduleRegion 中的指令进行重新排序。略。
在调度完成后,递归地为标量指令组生成相应的向量指令。为
%1, %2, %3, %4这 4 条LoadInst指令生成的向量化指令为%2 = load <4 x float>, <4 x float>* %1, align 4,为%mul2, %mul5, %mul10, %mul154 条FMulInst指令生成的向量化指令为%3 = fmul <4 x float> <float 7.000000e+00, float 7.000000e+00, float 7.000000e+00, float 7.000000e+00>, %2。因为本例中没有
ExternalUses,所以无需为ExternalUses生成ExtractElementInst指令。然后将
%mul2 + %mul5 + %mul10 + %mul15替换为对应的 split vector reduction:%rdx.shuf = shufflevector <4 x float> %3, <4 x float> undef, <4 x i32> <i32 2, i32 3, i32 undef, i32 undef> %bin.rdx = fadd fast <4 x float> %3, %rdx.shuf %rdx.shuf1 = shufflevector <4 x float> %bin.rdx, <4 x float> undef, <4 x i32> <i32 1, i32 undef, i32 undef, i32 undef> %bin.rdx2 = fadd fast <4 x float> %bin.rdx, %rdx.shuf1 %4 = extractelement <4 x float> %bin.rdx2, i32 0最后,删除
VectorizableTree中所有被向量化的标量指令。
vectorizeGEPIndices
以如下 LLVM IR 为例,分析 vectorizeGEPIndices 是如何向量化 GetElementPtrInst 的 index 的。

SLPVectorizer 会后序遍历
test()函数的所有基本块,对于每个基本块,首先收集种子指令集合 seed instructions,然后依次调用vectorizeStoreChains(),vectorizeChainsInBlock(),vectorizeGEPIndices()尝试向量化。对于本例,vectorizeStoreChains(),vectorizeChainsInBlock()没有任何效果,主要关注vectorizeGEPIndices()的流程。本例中只存在一个基本块,收集到的种子指令集合 seed instructions 为:
%g0 = getelementptr inbounds i32, i32* %r, i64 %sub0%g1 = getelementptr inbounds i32, i32* %r, i64 %sub1%g2 = getelementptr inbounds i32, i32* %r, i64 %sub2%g3 = getelementptr inbounds i32, i32* %r, i64 %sub3
这些
GetElementPtrInst都只有一个 i64 类型的 index,并且该 index 不是 contant。以上述
GetElementPtrInstseed instructions 的 index 作为参数,调用函数tryToVectorizeList()。调用函数
buildTree()来构建 SLP 树。 需要注意的是,SLP 树的根节点是GetElementPtrInstseed instructions 的 index 即%sub1, %sub2, %sub3, %sub4,而不是GetElementPtrInstseed instructions 本身。沿着 use-def 链不断添加节点至 SLP 树,构建出来的 SLP 树如上图 (c) 所示。
调用函数
buildExternalUses,记录ExternalUse如下:%sub0 = sub nsw i64 %x0, %y0的ExternalUse为%g0 = getelementptr inbounds i32, i32* %r, i64 %sub0%sub1 = sub nsw i64 %x1, %y1的ExternalUse为%g1 = getelementptr inbounds i32, i32* %r, i64 %sub1%sub2 = sub nsw i64 %x2, %y2的ExternalUse为%g2 = getelementptr inbounds i32, i32* %r, i64 %sub2%sub3 = sub nsw i64 %x3, %y3的ExternalUse为%g3 = getelementptr inbounds i32, i32* %r, i64 %sub3
调用函数
getTreeCost(),估算 SLP 树向量化后的代码在运行时的指令开销与原本的标量指令在运行时的指令开销的差值。具体的每一个 SLP 节点的 cost 已在上图 (c) 中标出。 整个 SLP 树的 cost = (-3 + -3 + -3) + 4 + 0 = -5,其中 ExtractCost 是 4,SpillCost 是 0。 ExtractCost = 0 是因为 target-specific cost model 计算ret double %mul3这一 ExternalUse 的 cost 为 0; SpillCost = 0 则是因此本例中没有需要额外的 spill 和 refill 操作。最后调用函数
vectorizeTree()进行向量化。首先会对所有的 ScheduleRegion 进行调度,即对 ScheduleRegion 中的指令进行重新排序。本例子中,ScheduleRegion 调度前后指令顺序没有变化。
在调度完成后,递归地为标量指令组生成相应的向量指令。
然后为
ExternalUses生成ExtractElementInst指令。举例说明,%sub3 = sub nsw i64 %x3, %y3的ExternalUse为%g3 = getelementptr inbounds i32, i32* %r, i64 %sub3,因为%sub3是向量后的%5 = sub nsw <4 x i64> %2, %4的 Lane 4 元素,所以额外生成%9 = extractelement <4 x i64> %5, i32 3并且将%g3 = getelementptr inbounds i32, i32* %r, i64 %sub3中的%sub3替换为%7即%g3 = getelementptr inbounds i32, i32* %r, i64 %9。最后,删除
VectorizableTree中所有被向量化的标量指令,被删除的标量指令在图 (b) 中标记为灰色。
Summary
本文浅析了 LLVM 中 SLP Vectorizer 的实现,可以看到还是与原始论文《Exploiting Superword Level Parallelism with Multimedia Instruction Sets》 中的算法有些不同的,论文中 SLP algorithm 是从识别 adjacent memory references 开始的,而 LLVM 中的实现则是 bottom-up SLP algorithm,是从收集 seed instructions 开始的。
本文对 LLVM SLP Vectorizer 的源码分析基于 LLVM release/4.x 版本,最新版本 LLVM 中的 SLP Vectorizer 与 release/4.x 版本相比已经做了非常多的改进了。也有一些学术论文中提出的 SLP 改进算法被 upstream 到 LLVM 的 SLP Vectorizer 中,例如:
LLVM 和 GCC 中的 SLP Vectorizer 都是在 Loop Vectorizer 之后执行的,关于开启 SLP Vectorizer 后能多大程度的提升应用程序性能也是可以关注的点。在 2013 LLVM Developers’ Meeting: “Vectorization in LLVM” - YouTube 的最后有人问道:
Q: Do you happen to know how the speed ups from the two vectorizers (Loop Vectorizer and SLP Vectorizer) split out? One of them is more important or is it kind of equal?
A: The loop vectorizer is a lot more important.